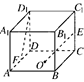
在棱长为2的正方体ABCD-A1B1C1D1中,O是底面ABCD的中心,E、F分别是CC1、AD的中点,那么异面直线OE和FD1所成的角的余弦值等于( )
A.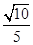 |
B. |
C.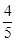 |
D.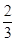 |
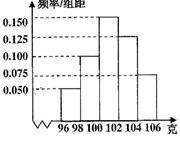
某工厂对一批产品进行了抽样检测.右图是根据
抽样检测后的产品净重数据绘制的频率分布直方
图,已知样本中产品净重小于100克的个数是36,
则样本中净重在[98,104)的产品的个数是( )
| A.90 | B.75 | C. 60 | D.45 |
某单位有职工160人,其中业务员有104人,管理人员32人,后勤服务人员24人,现用分层抽样法从中抽取一容量为20的样本,则抽取管理人员( )
| A.3人 | B.2人 | C.7人 | D.12人 |
从 个同类产品(其中
个同类产品(其中 个是正品,
个是正品, 个是次品)中任意抽取
个是次品)中任意抽取 个的必然事件是()
个的必然事件是()
A. 个都是正品 个都是正品 |
B.至少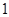 个是次品 个是次品 |
C. 个都是次品 个都是次品 |
D.至少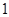 个正品 个正品 |
圆x2+y2-2x-2y+1=0上的点到直线 的距离的最大值是( )
的距离的最大值是( )
A. |
B.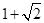 |
C. |
D. |
如图给出的是计算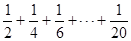 的值的一个程序框图,其中判断框内应填入的条件是()
的值的一个程序框图,其中判断框内应填入的条件是()
| A.i>10? | B.i<10? | C.i>20? | D.i<20? |
