（本小题10分）某宾馆客房部有60个房间供游客居住，当每个房间的定价为每天200元时，
房间可以住满。当每个房间每天的定价每增加10元时，就会有一个房间空闲。对有游客入住的房间，宾馆需对每个房间每天支出20元的各种费用。
设每个房间每天的定价增加
元，求：（1）房间每天的入住量
（间）关于（元）的函数关系式；（2）该宾馆每天的房间收费
（元）关于（元）的函数关系式；（3）该宾馆客房部每天的利润
（元）关于（元）的函数关系式；当每个房间的定价为每天多少元时，有最大值？最大值是多少
？
（2011山东济宁，21，8分）某市在道路改造过程中，需要铺设一条长为1000米的管道，决定由甲、乙两个工程队来完成这一工程.已知甲工程队比乙工程队每天能多铺设20米，且甲工程队铺设350米所用的天数与乙工程队铺设250米所用的天数相同.
（1）甲、乙工程队每天各能铺设多少米？
（2）如果要求完成该项工程的工期不超过10天，那么为两工程队分配工程量（以百米为单位）的方案有几种？请你帮助设计出来.
某品牌瓶装饮料每箱价格26元，某商店对该瓶装饮料进行“买一送三”促销活动，若整箱购买，则买一箱送三瓶，这相当于每瓶比原价便宜了0.6元．问该品牌饮料一箱有多少瓶？
解分式方程：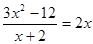
．
，6分）解方程：
解分式方程：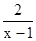
=