(本小题12分)如图,直线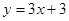 交
交 轴于A点,交
轴于A点,交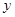 轴于B点,过A、B两点的抛物线交
轴于B点,过A、B两点的抛物线交 轴于另一点C(3,0).
轴于另一点C(3,0). 
⑴ 求抛物线的解析式;
⑵ 在抛物线的对称轴上是否存在点Q,使△ABQ是等腰三角形?若存在,求出符合条件的Q点坐标;若不存在,
 请说明理由.
请说明理由.
解方程: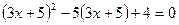 .
.
解方程: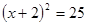 .
.
意大利著名数学家斐波那契在研究兔子繁殖问题时,发现有这样一组数:1,1,2,3,5,8,13,…,其中从第三个数起,每一个数都等于它前面两个数的和.现以这组数中的各个数作为正方形的边长值构造如下正方形: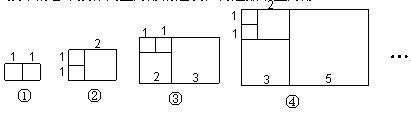
再分别依次从左到右取2个、3个、4个、5个…正方形拼成如下长方形并记为①、②、
③、④、 …相应长方形的周长如下表所示: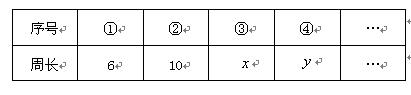
仔细观察图形,上表中的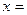 ,
,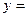 .
.
若按此规律继续作长方形,则序号为⑧的长方形周长是。
星期天小明在一条南北方向的公路上往返跑步,他从家里出发,每隔10分钟记录下自己的跑步情况(向南为正,单位:米)
-2080, 1100, -1120, 2010, 890, -940.
1小时后停下来休息,此时他在家的什么方向?最远距离家多远?小明回到家时共跑了多少米?
先化简,再求值①
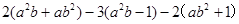 ,其中
,其中 .
.② 若 xy="5,x-y=3," 求 -7xy+5(x+y)-3xy-10y 的值