如图,Rt△ABC中∠C=90°、∠A=30°,在AC边上取点O画圆使⊙O经过A、B两点,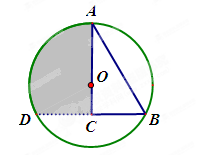
(1)求证:以O为圆心,以OC为半径的圆与AB相切.
(2) 下列结论正确的序号是 .(少选酌情给分,多选、错均不给分)
①AO =2CO ;
=2CO ;
②AO=BC;
③延长BC交⊙O与D,则A、B、D是⊙O的三等分点.
④图中阴影面积为: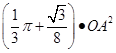
化简: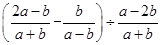 .
.
已知,纸片⊙O的半径为2,如图1,沿弦AB折叠操作.
(1)①折叠后的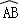 所在圆的圆心为O′时,求O′A的长度;
所在圆的圆心为O′时,求O′A的长度;
②如图2,当折叠后的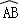 经过圆心为O时,求
经过圆心为O时,求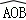 的长度;
的长度;
③如图3,当弦AB=2时,求圆心O到弦AB的距离;
(2)在图1中,再将纸片⊙O沿弦CD折叠操作.
①如图4,当AB∥CD,折叠后的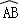 与
与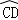 所在圆外切于点P时,设点O到弦AB.CD的距离之和为d,求d的值;
所在圆外切于点P时,设点O到弦AB.CD的距离之和为d,求d的值;
②如图5,当AB与CD不平行,折叠后的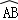 与
与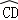 所在圆外切于点P时,设点M为AB的中点,点N为CD的中点,试探究四边形OMPN的形状,并证明你的结论.
所在圆外切于点P时,设点M为AB的中点,点N为CD的中点,试探究四边形OMPN的形状,并证明你的结论.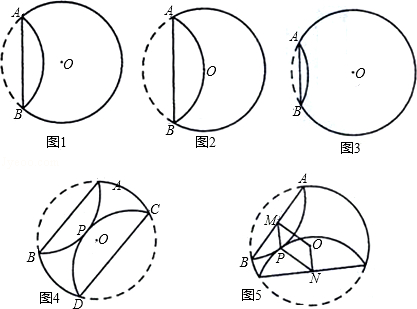
如图,已知二次函数L1:y=x2﹣4x+3与x轴交于A.B两点(点A在点B左边),与y轴交于点C.
(1)写出二次函数L1的开口方向、对称轴和顶点坐标;
(2)研究二次函数L2:y=kx2﹣4kx+3k(k≠0).
①写出二次函数L2与二次函数L1有关图象的两条相同的性质;
②若直线y=8k与抛物线L2交于E、F两点,问线段EF的长度是否发生变化?如果不会,请求出EF的长度;如果会,请说明理由.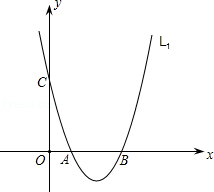
如图1,小红家阳台上放置了一个晒衣架.如图2是晒衣架的侧面示意图,立杆AB.CD相交于点O,B.D两点立于地面,经测量:
AB=CD=136cm,OA=OC=51cm,OE=OF=34cm,现将晒衣架完全稳固张开,扣链EF成一条直线,且EF=32cm.
(1)求证:AC∥BD;
(2)求扣链EF与立杆AB的夹角∠OEF的度数(精确到0.1°);
(3)小红的连衣裙穿在衣架后的总长度达到122cm,垂挂在晒衣架上是否会拖落到地面?请通过计算说明理由.
(参考数据:sin61.9°≈0.882,cos61.9°≈0.471,
tan61.9°≈0.553;可使用科学记算器)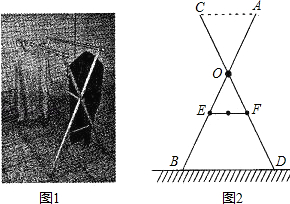
我们约定:如果身高在选定标准的±2%范围之内都称为“普通身高”.为了了解某校九年级男生中具有“普遍身高”的人数,我们从该校九年级男生中随机抽出10名男生,分别测量出他们的身高(单位:cm),收集并整理如下统计表:
(1)计算这组数据的三个统计量:平均数、中位数、众数;
(2)请你选择其中一个统计量作为选定标准,找出这10名男生中具有“普遍身高”是哪几位男生?并说明理由.