某课题小组对课本的习题进行了如下探索，请逐步思考并解答：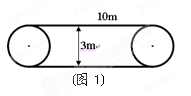
（1）（人教版教材习题24.4的第2题）如图1，两个大小一样的传送轮连接着一条传送带，两个传动轮中心的距离是10m，求这条传送带的长_________.（2）改变图形的数量;
如图2、将传动轮增加到3个，每个传动轮的直径是3m,每两个传动轮中心的距离是10m, 求这条传送带的长__________.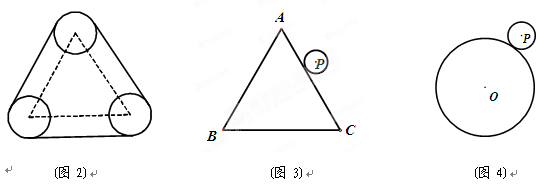
（
3）改变动态关系，将静态问题升华为动态问题：
如图3，一个半径为1cm的⊙P沿边长为2πcm的等边三角形△ABC的外沿作无滑动滚动一周,求圆心P经过的路径长？⊙P自转了多少周？(4) 拓展与应用
如图4，一个半径为1cm的⊙P沿半径为3cm的⊙O外沿作无滑动滚动一周,则⊙P自转了多少周？
（本小题满分6分）经过某十字路口的汽车，它可能继续直行，也可能向左转或向右转，这三种可能性大小相同，现在两辆汽车经过这个十字路口．
（1）请用“树形图”或“列表法”列举出这两辆汽车行驶方向所有可能的结果；
（2）求这两辆汽车都向左转的概率．
（本小题满分6分）
如图，九年级（1）班课外活动小组利用标杆测量学校旗杆的高度，已知标杆高度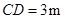
，标杆与旗杆
的水平距离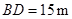
，人的眼睛与地面的高度
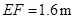，人与标杆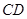
的水平距离
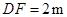，人的
眼睛E、标杆顶点C和旗杆顶点A在同一直线，求旗杆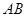
的高度．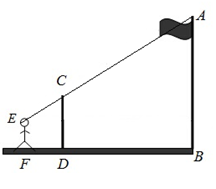
（本小题满分8分，每题4分）
（1）不解方程，判断方程
根的情况.
（2）求抛物线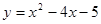
与x轴的两个交点坐标.
如图，在平面直角坐标系中，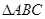
的三个顶点坐标分别为
(
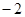，1)，
(
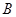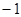，4)，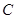
(
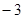，2)．以原点
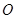为位似中心，位似比为1:2，在
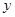轴的左侧，画出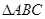放大后的图形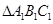
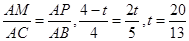，并直接写出
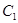点坐标；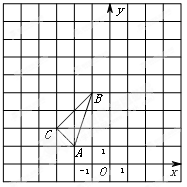 
已知：如图，菱形ABCD中，对角线AC，BD相交于点O，且AC=12cm，BD=16cm．点P从点B出发，沿BA方向匀速运动，速度为1cm/s；同时，直线EF从点D出发，沿DB方向匀速运动，速度为1cm/s，EF⊥BD，且与AD，BD，CD分别交于点E，Q，F；当直线EF停止运动时，点P也停止运动．连接PF，设运动时间为t（s）（0＜t＜8）．解答下列问题：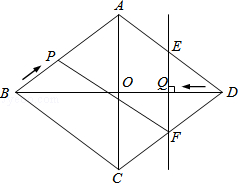
（1）当t为何值时，四边形APFD是平行四边形？
（2）设四边形APFE的面积为y（cm2），求y与t之间的函数关系式；
（3）是否存在某一时刻t，使S四边形APFE：S菱形ABCD=17：40？若存在，求出t的值，并求出此时P，E两点间的距离；若不存在，请说明理由．