(13分)如图，在△ABC中，AB＝AC＝5，BC＝6，点D为AB边上的一动点(D不与A、B重合)，过D作DE∥BC，交AC于点E．把△ADE沿直线DE折叠，点A落在点A'处．连结BA'，设AD＝x，△ADE的边DE上的高为y．(1) 求出y与x的函数关系式；
(2) 若以点A'、B、D为顶点的三角形与△ABC 相似，求x的值；
(3) 当x取何值时，△A' DB是直角三角形．
先化简，再求值：
，其中m=1+
．
（1）计算：
；
（2）解方程：
．
计算：
（1）
﹣|
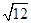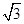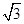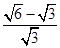﹣3|+（）2；
（2）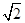
+（2+
）（2﹣）．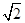
宜兴紧靠太湖，所产百合有“太湖人参”之美誉，今年百合上市后，甲、乙两超市分别用12000元以相同的进价购进质量相同的百合，甲超市销售方案是：将百合按分类包装销售，其中挑出优质的百合400千克，以进价的2倍价格销售，剩下的百合以高于进价10%销售．乙超市的销售方案是：不将百合分类，直接包装销售，价格按甲超市分类销售的两种百合售价的平均数定价．若两超市将百合全部售完，其中甲超市获利8400元（其它成本不计）．问：
（1）百合进价为每千克多少元？
（2）乙超市获利多少元？并比较哪种销售方式更合算．
如图，点B（3，3）在双曲线y=
（x＞0）上，点D在双曲线y=﹣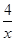
（x＜0）上，点A和点C分别在x轴、y轴的正半轴上，且点A、B、C构成的四边形为正方形．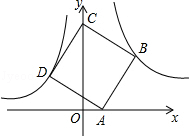
（1）求k的值；
（2）求点A的坐标．