已知二次函数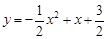
． (1)用配方法将函数解析式化为y=a(x-h)2+k的形式；
(2)当x为何值时，函数值y=0；
(3)列表描点，在所给坐标系中画出该函数的图象；
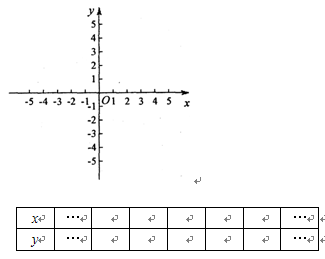
(4)观察图象，指出使函数值
y＞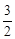
时自变量x的取值范围．
分解因式：
（1）3x（a﹣b）﹣2y（b﹣a）
（2）﹣2a3+12a2﹣18a
（3）4+12（x﹣y）+9（x﹣y）2
（4）4a2﹣9（b﹣1）2．
把下列各式分解因式：
①3（a+b）2﹣27c2
②16（x+y）2﹣25（x﹣y）2
③a2（a﹣b）+b2（b﹣a）
④（5m2+3n2）2﹣（3m2+5n2）2
分解因式：
（1）a2x2y﹣axy2（2）x（x﹣y）﹣y（y﹣x）
（3）9（a﹣b）2﹣16（a+b）2（4）25（x﹣y）2+10（y﹣x）+1
（5）﹣3x3+12x2y﹣12xy2（6）m（x﹣y）2﹣x+y．
把下列各式分解因式
（1）12a3b2﹣9a2b+3ab；
（2）a（x+y）﹣（a﹣b）（x+y）；
（3）121x2﹣144y2；
（4）4（a﹣b）2﹣（x﹣y）2；
（5）（x﹣2）2+10（x﹣2）+25；
（6）a3（x+y）2﹣4a3c2．
因式分解：（1）4a3b2﹣6a2b3+2a2b2= ，
（2）﹣x2+2xy﹣y2= ．