已知
是两个不同的平面，m、n是平面
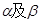之外的两条不同的直线，给出四个论断： ①m⊥n，②
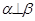，③
，④
。
以其中三个论断作为条件，余下一个论断作为结论，写出你认为正确的一个命题________。
给出如下四个命题：
①方程x2＋y2－2x＋1＝0表示的图形是圆；
②若椭圆的离心率为，则两个焦点与短轴的两个端点构成正方形；
③抛物线x＝2y2的焦点坐标为；
④双曲线－＝1的渐近线方程为y＝±x.
其中正确命题的序号是_______
椭圆＋＝1(a>b>0)的两个焦点是F1(－c,0)、F2(c,0)，M是椭圆上一点，且F1M·＝0，则离心率e的取值范围是________
以双曲线－＝1的中心为顶点，且以该双曲线的右焦点为焦点的拋物线方程是__________
已知点F(1,0)，直线l：x＝－1，点P为平面上的动点，过点P作直线l的垂线，垂足为点Q，且·＝·，则动点P的轨迹C的方程是______
先后拋掷两枚均匀的正方体骰子(它们的六个面分别标有点数1,2,3,4,5,6)，骰子朝上的面的点数分别为x、y，则log2xy＝1的概率为____