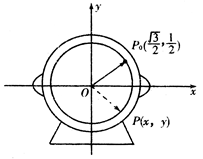
如图,为了研究钟表与三角函数的关系,建立如图所示的坐标系,设秒针尖位置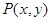 .若初始位置为
.若初始位置为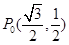 ,当秒针从
,当秒针从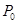 (注此时
(注此时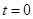 )正常开始走时,那么点P的纵坐标y与时间t的函数关系为
)正常开始走时,那么点P的纵坐标y与时间t的函数关系为
A.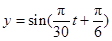 |
B.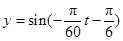 |
C.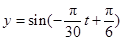 |
D.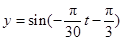 |
棱长为a的正方体中,连结相邻面的中心,以这些线段为棱的八面体的体积为()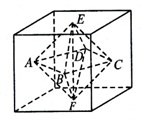
A.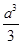 |
B.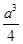 |
C. |
D.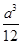 |
已知α,β表示两个不同的平面,m为平面α内的一条直线,则“ ”是“
”是“ ”的
”的
| A.充分不必要条件 | B.必要不充分条件 |
| C.充要条件 | D.既不充分也不必要条件 |
如图,在半径为3的球面上有A、B、C三点,∠ABC=900,BA=BC,球心 到平面ABC的距离是
到平面ABC的距离是 ,则B、C两点的球面距离是
,则B、C两点的球面距离是 
A、 B、
B、 C、
C、 D、
D、
如图,已知六棱锥P-ABCDEF的底面是正六边形,PA⊥平面ABC,PA=2AB,则下列结论正确的是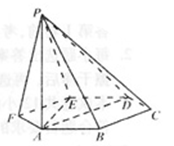
| A.PB⊥AD | B.平面PAB⊥平面PBC |
| C.直线BC∥平面PAE | D.直线PD与平面ABC所成角为450 |
正方体 --
-- ,E、F分别是
,E、F分别是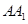 、
、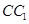 的中点,p是
的中点,p是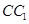 上的动点(包括端点),过E、D、P作正方体的截面,若截面为四边形,则P的轨迹是
上的动点(包括端点),过E、D、P作正方体的截面,若截面为四边形,则P的轨迹是
A、线段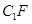 B、线段
B、线段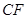
C、线段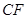 和一点
和一点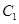 D、线段
D、线段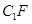 和一点C
和一点C