设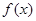 为定义在
为定义在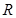 上的奇函数,当
上的奇函数,当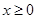 时,
时, 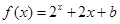 (
(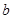 为常数),则
为常数),则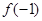 =( )
=( )
| A.3 | B.1 | C.-1 | D.-3 |
过椭圆 +
+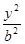 =1(0<b<a)中心的直线与椭圆交于A、B两点,右焦点为F2(c,0),则△ABF2的最大面积是()
=1(0<b<a)中心的直线与椭圆交于A、B两点,右焦点为F2(c,0),则△ABF2的最大面积是()
A.ab
B.ac
C.bc
D.b2
过双曲线 的右焦点F作直线l交双曲线于A、B两点,若|AB|=4,则这样的直线l有()
的右焦点F作直线l交双曲线于A、B两点,若|AB|=4,则这样的直线l有()
A.1条
B.2条
C.3条
D.4条
中心在原点,焦点坐标为(0, ±5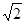 )的椭圆被直线3x-y-2=0截得的弦的中点的横坐标为
)的椭圆被直线3x-y-2=0截得的弦的中点的横坐标为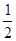 ,则椭圆方程为()
,则椭圆方程为()
A. + +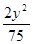 =1 =1 |
B.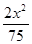 + + =1 =1 |
C.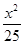 + + =1 =1 |
D. + +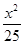 =1 =1 |
设双曲线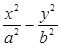 =1(0<a<b=的半焦距为c,直线l过(a,0),(0,b)两点.已知原点到直线l的距离为
=1(0<a<b=的半焦距为c,直线l过(a,0),(0,b)两点.已知原点到直线l的距离为 c,则双曲线的离心率为()
c,则双曲线的离心率为()
| A.2 | B.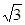 |
C. |
D. |
x= 表示的曲线是()
表示的曲线是()
| A.双曲线 | B.椭圆 |
| C.双曲线的一部分 | D.椭圆的一部分 |