(1)小明说:“请你任意想一个数,把这个数乘2后加8,然后除以4,再减去你原来所想的那个数的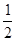 ,我可以知道你计算的结果是2.”
,我可以知道你计算的结果是2.”
请你帮助小明说明上述结论的正确性.
如果设任意想的那个数为x,则根据题意,得代数式(请完善下面的解题过程):
(2)在(1)中,得到的代数式化简后结果为2,它不含有x,我们称之为“与x无关”.
试解决下列“无关”类问题:
①多项式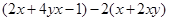 的值()
的值()
| A.仅与x的大小无关 | B.仅与y的大小无关 |
| C.与x、y的大小都无关 | D.与x、y的大小都有关 |
②如果已知代数式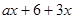 的值与其中某个字母的取值无关,你能求出哪一个字母的值?此时这个字母的值是多少?
的值与其中某个字母的取值无关,你能求出哪一个字母的值?此时这个字母的值是多少?
(本题4分) 甲、乙两家文具商店出售同样的毛笔和宣纸.毛笔每支18元,宣纸每张2元.甲商店推出的优惠方法为买一支毛笔送一张宣纸;乙商店的优惠方法为按总价的九折优惠.小丽想购买5支毛笔,宣纸 张(
张( )
)
(1)若到甲商店购买,应付 元(用代数式表示).
(2)若到乙商店购买,应付 元(用代数式表示).
(3)若小丽要买宣纸20张,应选择哪家商店?
(本题5分)有理数 、
、 、
、 在数轴上的位置如图:
在数轴上的位置如图:
(1)判断正负,用“<”或“>”填空:c-b 0, a+b 0, a-c 0.
(2)化简: .
.
(本题5分)已知a、b互为相反数,c、d互为倒数,m为平方得本身的数.求代数式: 的值.
的值.
先化简,再求值:(本题4分) ,其中:
,其中: ,
,  .
.