某市种植某种绿色蔬菜，全部用来出口．为了扩大出口规模，该市决定对这种蔬菜的种植实行政府补贴，规定每种植一亩这种蔬菜一次性补贴菜农若干元．经调查，种植亩数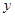
（亩）与补贴数额
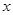（元）之间大致满足如图1所示的一次函数关系．随着补贴数额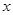的不断增大，出口量也不断增加，但每亩蔬菜的收益
（元）会相应降低，且与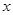之间也大致满足如图2所示的一次函数关系．在政府未出台补贴措施前，该市种植这种蔬菜的总收益额为多少？
求政府补贴政策实施后，种植亩数
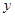、每亩蔬菜的收益分别与政府补贴数额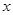之间的函数关系式；要使全市种植这种蔬菜的总收益
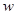（元）最大，政府应将每亩补贴数额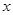定为多少？并求出总收益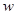的最大值．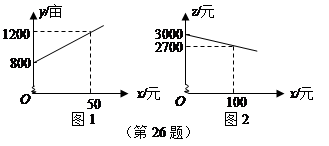
已知某种水果的批发单价与批发量的函数关系如图所示．
（1）请说明图中①、②两段函数图象的实际意义．
（2）写出批发该种水果的资金金额w（元）与批发量m（kg）之间的函数关系式；在下图的坐标系中画出该函数图象；指出金额在什么范围内，以同样的资金可以批发到较多数量的该种水果．
某地举办乒乓球比赛的费用y（元）包括两部分：一部分是租用比赛场地等固定不变的费用b，另一部分与参加比赛的人数x（人）成正比例． 当x＝20时，y＝1600，当x＝30时，y＝2000．
（1）求y与x之间的函数关系式；
（2）如果有50名运动员参加比赛，且全部费用由运动员分摊，那么每名运动员需要支付多少元？
已知一次函数y=kx+b的图象经过点（﹣1，﹣5），且与正比例函数
的图象相交于点（2 ，a）．
（1）求一次函数y=kx+b的表达式；
（2）在同一坐标系中，画出这两个函数的图象，并求这两条直线与y轴围成的三角形的面积．
如图，在四边形ABCD中，AB=BC，BF是∠ABC的平分线，AF∥DC，连接AC、CF，求证：（1）FA=FC.（2）CA是∠DCF的平分线.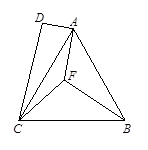
如图，点E、F在AB上，且AF＝BE，AC＝BD，AC∥BD．求证：CF∥DE．