如图①,在平面直角坐标系中,已知△ABC是等边三角形,点B的坐标为(12,0),动点P在线段AB上从点A向点B以每秒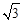 个单位的速度运动,设运动时间为t秒.以点P为顶点,作等边△PMN,点M,N在x轴上.
个单位的速度运动,设运动时间为t秒.以点P为顶点,作等边△PMN,点M,N在x轴上.
当t为何值时,点M与点O重合.
求点P坐标和等边△PMN的边长(用t的代数式表示).
如果取OB的中点D,以OD为边在△AOB内部作如图②所示的矩形ODEF,点E在线段AB上.设等边△PMN和矩形ODEF重叠部分的面积为S,请求出当
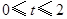 秒时S与
秒时S与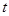 的函数关系式,并求出S的最大值.
的函数关系式,并求出S的最大值.
为了了解中学生的体能情况,抽取了某中学八年级学生进行跳绳测试,将所得数据整理后,画出如图所示的频率分布直方图,已知图中从左到右前三个小组的频率分别是0.1,0.3,0.4,第一小组的频数为5。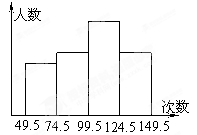
(1)第四小组的频率是__________;
(2)参加这次测试的学生是_________人;
(3)成绩落在哪组数据范围内的人数最多?是多少?
(4)求成绩在100次以上(包括100次)的学生占测试人数的百分率.
解方程: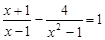
已知x=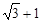 ,y=
,y=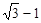 ,求
,求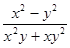 的值.
的值.
解不等式组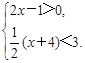 并把解集在数轴上表示出来.
并把解集在数轴上表示出来.
某食品加工厂要把600吨方便面包装后送往灾区。
(1)写出包装所需的天数t天与包装速度 y 吨/天的函数关系式;
(2)包装车间有包装工120名,每天最多包装60吨,预计最快需要几天才能包装完?
(3)包装车间连续工作7天后,为更快地帮助灾区群众,厂方决定在2天内把剩余的方便面全部包装完毕,问需要调来多少人支援才能完成任务?