设二次函数f(x)=mx2+nx+t的图像过原点,g(x)=ax3+bx−3(x>0),f(x), g(x)的导函数为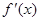 ,g¢(x),且
,g¢(x),且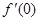 ="0,"
="0,"  =−2,f(1)="g(1),"
=−2,f(1)="g(1)," 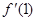 =g¢(1).
=g¢(1).
(Ⅰ)求函数f(x),g(x)的解析式;
(Ⅱ)求F(x)=f(x)−g(x)的极小值;
(Ⅲ)是否存在实常数k和m,使得f(x)³kx+m和g(x)£kx+m成立?若存在,求出k和m的值;若不存在,说明理由.
(本小题满分12分)
如图,在斜边为AB的Rt△ABC,过A作PA⊥平面ABC,AE⊥PB于E,AF⊥PC于F.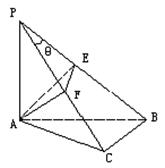
(1)求证:BC⊥平面PAC.
(2)求证:PB⊥平面AEF.
(3)若AP=AB=2,试用tgθ(∠BPC=θ)表示△AEF的面积、当tgθ取何值时,△AEF的面积最大?最大面积是多少?
(本小题满分12分)
如图,DC⊥平面ABC,EB∥DC,AC=BC=EB=2DC=2,∠ACB=120°,P、Q分别为AE、AB的中点.
(1)证明:PQ∥平面ACD;
(2)求AD与平面ABE所成角的正弦值.
(本小题满分12分)
P为正方形ABCD所在平面外一点,PA⊥面ABCD,AE⊥PB,求证:AE⊥PC.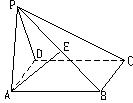
(本小题满分13分)
在△ABC中,AB=AC=5,BC=6,PA⊥平面ABC,PA=8,求点P到BC的距离.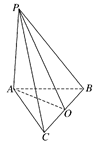
(本小题满分13分)
空间四边形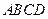 中,
中,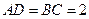 ,
, 分别是
分别是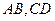 的中点,
的中点,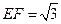 ,求异面直线
,求异面直线 所成的角.
所成的角.