在2012年元旦期间有甲、乙两个小型超市举行有奖促销活动,顾客每购货20元就有一回按下面规则转盘获奖机会,且两超市奖额等同.规则是甲、乙两超市各把一转盘分成4个、3个区域,并标上了数字(如图甲、乙),顾客一回转盘要转两次,第一次与第二次分别停止后指针所指数字之和为奇数时就获奖(若指针停在等分线上,那么重转一次,直到指针指向某一份为止).利用树形图或列表法分别求出甲、乙两超市顾客一回转盘获奖的概率;
如果只考虑中奖因素,你将会选择去哪个超市购物?请说明理由.

在平面直角坐标系xOy中,直线y=-x+3与两坐标轴围成一个△AOB.现将背面完全相同,正面分别标有数l、2、3、 、
、 的5张卡片洗匀后,背面朝上,从中任取一张,将该卡片上的数作为点P的横坐标,再在剩下的4张卡片中任取一张,将该卡片上的数作为点P的纵坐标,请用所学的知识求出点P落在△AOB内部的概率.
的5张卡片洗匀后,背面朝上,从中任取一张,将该卡片上的数作为点P的横坐标,再在剩下的4张卡片中任取一张,将该卡片上的数作为点P的纵坐标,请用所学的知识求出点P落在△AOB内部的概率.
“知识改变命运,科技繁荣祖国”.我区中小学每年都要举办一届科技比赛.下图为我区某校
2010年参加科技比赛(包括电子百拼、航模、机器人、建模四个类别)的参赛人数统计图
(1)该校参加机器人、建模比赛的人数分别是人和人;
(2)该校参加科技比赛的总人数是人,电子百拼所在扇形的圆心角的度数是°,并把条形统计图补充完整;
(3)从全区中小学参加科技比赛选手中随机抽取80人,其中有32人获奖. 今年我区中小学参加科技比赛人数共有2485人,请你估算今年参加科技比赛的获奖人数约是多少人?

已知如图在平行四边形ABCD中,E、F分别为边AB、CD的中点,BD是对角线,AG∥BD交CB的延长线于G.
(1)求证:△ADE≌△CBF;
(2)若四边形BEDF是菱形,则四边形AGBD是什么特殊四边形?并证明你的结论。
解方程组:
在△ABC中,D为BC的中点,E为AC上任一点,BE交AD于O,某学生在研究这一问题时,发现了如下事实: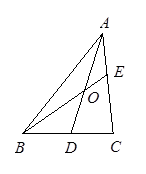
(1)当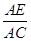 =
=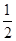 =
=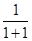 时,有
时,有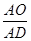 =
=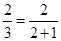 ;
;
(2)当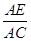 =
=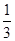 =
=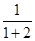 时,有
时,有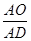 =
=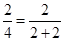 ;
;
(3)当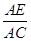 =
=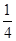 =
=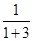 时,有
时,有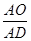 =
=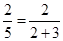 ;
;
1)当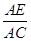 =
=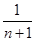 时,按照上述的结论,请你猜想
时,按照上述的结论,请你猜想
用n表示AO/AD的一般性结论(n为正整数);
2)若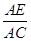 =
=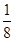 ,且AD=18,求AO.
,且AD=18,求AO.