已知:如图,在△ABC中,CD⊥AB垂足为D,BE⊥AC垂足为E,连接DE,点G、F分别是BC、DE的中点.
求证:GF⊥DE.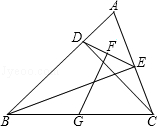
如图,已知△ABC是等边三角形,BD是△ABC的中线,延长BC至E,使CE=CD,连接DE,试说明BD=ED的理由.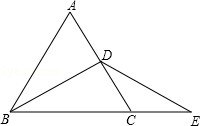
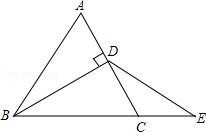
如图,BD是等边△ABC的高,E是BC延长线上一点,且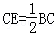 .
.
(1)直接写出CE与CD的数量关系;
(2)试说明△BDE是等腰三角形.
如图,在△ABC中,∠B=∠C=30°,D是BC的中点,连接AD,求∠BAD与∠ADC的度数.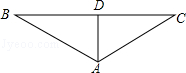
如图:在△ACB中,点D是AB边上一点,且∠ACB=∠CDA,∠CAB的平分线分别交CD、BC于点E、F.
(1)作出∠CAB的平分线AE;
(2)试说明△CEF是什么三角形?并证明你的结论.