设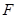
是抛物线C1：y2＝2px (p＞0) 的焦点，点A是抛物线与双曲线C2：
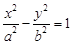(a＞0，b＞0)的一条渐近线的一个公共点，且AF⊥x轴，则双曲线的离心率为（ ▲ ）
| A．2 | B． |
C． |
D． |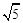
给出右面的程序框图，那么输出的数是（）
| A．2450 | B．2550 | C．5050 | D．4900 |
已知定义在R上的奇函数f(x)和偶函数g(x)满足f(x)+g(x)=ax－a-x+2（a>0且a≠1）若g(2)=a则f(2)=( )
| A．2 | B． |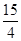
C． |
D．a2 |
复数
的实部与虚部之和为（）
| A．0 | B． |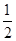
C．1 | D．2 |
设O为坐标原点，
是双曲线
的焦点，若在双曲线上存在点P，使得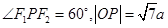
，则双曲线的渐近线方程为（）
A． |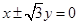
B． |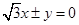
C． |
D． |
某五所大学进行自主招生，同时向一所重点中学的五位学习成绩优秀，并在某些方面有特长的发出提前录取通知单，若这五名学生都乐意进这五所大学中的任意一所就读，则仅有两名学生录取到同一所大学（其余三人在其他学校各选一所不同大学）的概率是（）
A． |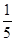
B． |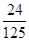
C． |
D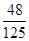． |