已知f(x)=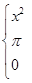
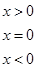 ,则f [ f (-3)]等于
,则f [ f (-3)]等于
| A.0 | B.π | C.π2 | D.9 |
方程3x+x=3的解所在的区间为:
| A.(0,1) | B.(1,2) | C.(2,3) | D.(3,4) |
在空间中,a,b是不重合的直线,α,β是不重合的平面,则下列条件中可推出a∥b的是:
A.a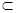 α,b α,b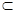 β α∥β β α∥β |
B.a⊥α b⊥α |
C.a∥αb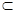 α α |
D.a⊥α b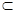 α α |
有一个几何体的三视图及其尺寸如下(单位:cm),其侧视图和主视图是全等的三角形,则该几何体的表面积为: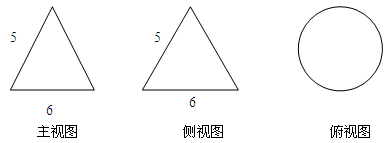
| A.12cm2 | B.15πcm2 | C.24πcm2 | D.36πcm2 |
下列各组函数中表示同一函数的是:
A.f(x)=x与g(x)=( )2 )2 |
B.f(x)=lnex与g(x)=elnx |
C.f(x)= ,与g(x)= ,与g(x)=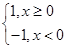 |
D.f(x)=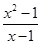 与g(t)=t+1(t≠1) 与g(t)=t+1(t≠1) |