已知二次函数 的图象如图所示,它与x轴的一个交点的坐标为(-1,0),与y轴的交点坐标为(0,-3).
的图象如图所示,它与x轴的一个交点的坐标为(-1,0),与y轴的交点坐标为(0,-3).
(1)求此二次函数的解析式;
(2)求此二次函数的图象与x轴的另一个交点的坐标;
(3)根据图象回答:当x取何值时,y<0?
(南宁)如图,AB是⊙O的直径,C,G是⊙O上两点,且AC=CG,过点C的直线CD⊥BG于点D,交BA的延长线于点E,连接BC,交OD于点F.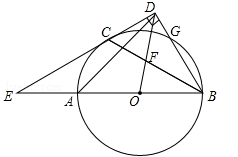
(1)求证:CD是⊙O的切线.
(2)若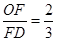 ,求∠E的度数.
,求∠E的度数.
(3)连接AD,在(2)的条件下,若CD=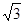 ,求AD的长.
,求AD的长.
(南宁)如图,在▱ABCD中,E、F分别是AB、DC边上的点,且AE=CF,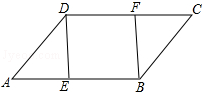
(1)求证:△ADE≌△CBF;
(2)若∠DEB=90°,求证:四边形DEBF是矩形.
(南宁)计算: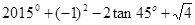 .
.
(贺州)如图,AB是⊙O的直径,C为⊙O上一点,AC平分∠BAD,AD⊥DC,垂足为D,OE⊥AC,垂足为E.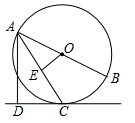
(1)求证:DC是⊙O的切线;
(2)若OE= cm,AC=
cm,AC= cm,求DC的长(结果保留根号).
cm,求DC的长(结果保留根号).
(贺州)如图,将矩形ABCD沿对角线BD对折,点C落在E处,BE与AD相交于点F.若DE=4,BD=8.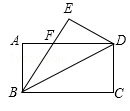
(1)求证:AF=EF;
(2)求证:BF平分∠ABD.