已知二次函数 y=ax2-x+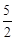 的图象经过点(-3, 1).
的图象经过点(-3, 1).
(1)求 a 的值;
(2)判断此函数的图象与x轴是否相交?如果相交,请求出交点坐标;
(3)画出这个函数的图象.(不要求列对应数值表,但要求尽可能画准确)
在 ABCD中,E、F分别是AB、CD的中点,连接AF、CE.
ABCD中,E、F分别是AB、CD的中点,连接AF、CE.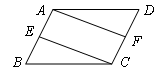
(1)求证:△BEC≌△DFA;
(2)连接AC,当CA=CB时,判断四边形AECF是什么特殊四边形?并证明你的结论.
为增强环保意识,某社区计划开展一次“减碳环保,减少用车时间”的宣传活动,对部分家庭五月份的平均每天用车时间进行了一次抽样调查,并根据收集的数据绘制了下面两幅不完整的统计图.请根据图中提供的信息,解答下列问题: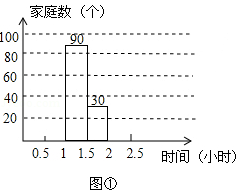

(1)本次抽样调查了多少个家庭?
(2)将图①中的条形图补充完整,直接写出用车时间的中位数落在哪个时间段内;
(3)求用车时间在1~1.5小时的部分对应的扇形圆心角的度数;
(4)若该社区有车家庭有1600个,请你估计该社区用车时间不超过1.5小时的约有多少个家庭?
(1)计算:
(2)化简分式 ,并从
,并从 中选一个你认为适合的
中选一个你认为适合的
整数 代人求值.
代人求值.
如图,在梯形ABCD中,AD∥BC,∠B=90°,BC=6,AD=3,∠DCB=30°.点E、F同时从B点出发,沿射线BC向右匀速移动.已知F点移动速度是E点移动速度的2倍,以EF为一边在CB的上方作等边△EFG.设E点移动距离为x(x>0).
⑴△EFG的边长是____(用含有x的代数式表示),当x=2时,点G的位置在_______;
⑵若△EFG与梯形ABCD重叠部分面积是y,求
①当0<x≤2时,y与x之间的函数关系式;
②当2<x≤6时,y与x之间的函数关系式;
⑶探求⑵中得到的函数y在x取何值时,存在最大值,并求出最大值.
如图所示,已知A点的坐标为(0,3),⊙A的半径为1,点B在 轴上.
轴上.
①若点B的坐标为(4,0),⊙B的半径为3,试判断⊙A与⊙B的位置关系;
②能否在 轴的正半轴上确定一点B,使⊙B与y轴相切,并且与⊙A相切?请说明理由.
轴的正半轴上确定一点B,使⊙B与y轴相切,并且与⊙A相切?请说明理由.