某学校为了调查高三年级的200名文科学生完成课后作业所需时间,采取了两种抽样调查的方式:第一种由学生会的同学随机抽取20名同学进行调查;第二种由教务处对该年级的文科学生进行编号,从001到200,抽取学号最后一位为2的同学进行调查,则这两种抽样的方法依次为( )
| A．分层抽样,简单随机抽样 | B．简单随机抽样, 分层抽样 |
| C．分层抽样,系统抽样 | D．简单随机抽样,系统抽样 |
设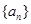
是等差数列，若
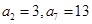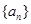,则数列前8项的和为( )
| A．128 | B．80 | C．64 | D．56 |
若函数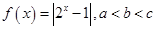
且
，则下列结论中，必成立的是( )
A． |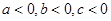
B． |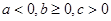
C． |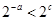
D． |
设函数
是定义在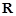
上的奇函数，且当
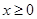时，单调递减，若数列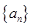
是等差数列，且
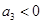，则
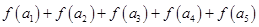的值（）
| A．恒为正数 | B．恒为负数 | C．恒为0 | D．可正可负 |
若函数
在
处有最小值，则
( )
A． |
B． |
C．4 | D．3 |
右图是函数
在区间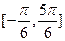
上的图象。为了得到这个函数的图象，只要将
的图象上所有的点（）
A．向左平移 个单位长度，再把所得各点的横坐标缩短到原来的 倍，纵坐标不变 |
| B．向左平移个单位长度，再把所得各点的横坐标伸长到原来的2倍，纵坐标不变 |
C．向左平移 个单位长度，再把所得各点的横坐标缩短到原来的倍，纵坐标不变 |
| D．向左平移个单位长度，再把所得各点的横坐标伸长到原来的2倍，纵坐标不变 |