（本小题满分6分）
如图，在△ABC中，∠ACB=90°，O为BC边上一点，以O为圆心，OB为半径作半圆与AB边和BC边分别交于点D、点E，连接CD，且CD=CA，BD=
，tan∠ADC=2．
（1）求证：CD是半圆O的切线
（2）求半圆O的直径；
（3）求AD的长.
(本题8分)关于x的一元二次方程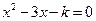
有两个不相等的实数根．
（1）求k的取值范围．
（2）请选择一个k的负整数值，并求出方程的根．
(每小题6分，共18分)解下列方程：
①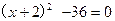
②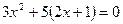
③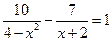
（本题12分）
如果一个正整数能表示为两个连续偶数的平方差，那么称这个正整数为“神秘数”．如：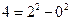
，
，
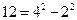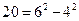，因此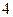
，
，
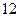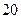这三个数都是神秘数．
（1）
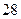和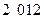
这两个数是神秘数吗？为什么？
（2）设两个连续偶数为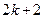
和
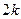（其中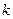
取非负整数），由这两个连续偶数构造的神秘数是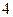的倍数吗？为什么？
（3）两个连续奇数的平方差（取正数）是神秘数吗？为什么？
（本题10分）
（1）拼一拼，画一画：请你用4个长为a，宽为b的矩形拼成一个大正方形，并且正中间留下一个洞，这个洞恰好是一个小正方形。
（2）用不同方法计算中间的小正方形的面积，聪明的你能发现什么？
（3）当拼成的这个大正方形边长比中间小正方形边长多3cm时，它的面积就多24cm2，求中间小正方形的边长。
（本题10分）如图4，边长为
的矩形，它的周长为14，面积为10，求下列各式的值：(1)
(2) 
29.
|
