如果若干个函数的图象经过平移后能够重合,则称这些函数为“互为生成函数”。给出下列函数① ;②
;②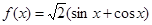 ;③
;③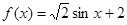 ;④
;④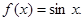 其中“互为生成函数”的是()
其中“互为生成函数”的是()
| A.①② | B.①③ | C.③④ | D.②④ |
已知函数 (
(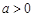 ,且
,且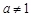 )的图象恒过定点,若点在一次函数
)的图象恒过定点,若点在一次函数 的图象上,其中
的图象上,其中 ,则
,则 的最小值为()
的最小值为()
| A.4 | B. |
C.2 | D.1 |
已知 是实数,则函数
是实数,则函数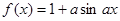 的图象不可能是()
的图象不可能是()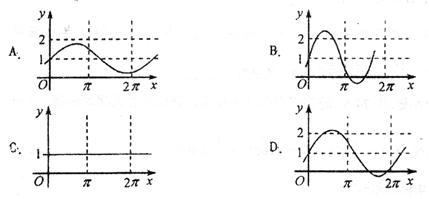
下列有关命题的说法正确的是
A.命题“若 ,则 ,则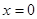 ”的否命题为:“若 ”的否命题为:“若 ,则 ,则 ” ” |
B.“若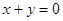 ,则 ,则 , ,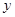 互为相反数”的逆命题为真命题 互为相反数”的逆命题为真命题 |
C.命题“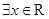 ,使得 ,使得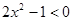 ”的否定是:“ ”的否定是:“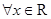 ,均有 ,均有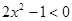 ” ” |
D.命题“若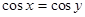 ,则 ,则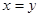 ”的逆否命题为真命题 ”的逆否命题为真命题 |
设函数 ,则
,则 ()
()
A.在区间 内均有零点 内均有零点 |
B.在区间 内均无零点 内均无零点 |
C.在区间 内有零点,在区间 内有零点,在区间 内无零点 内无零点 |
D.在区间 内无零点,在区间 内无零点,在区间 内有零点 内有零点 |