(本小题满分12分)
已知椭圆 过点
过点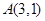 ,左、右焦点分别为
,左、右焦点分别为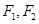 ,离心率为
,离心率为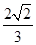 ,经过
,经过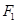 的直线
的直线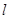 与圆心在
与圆心在 轴上且经过点
轴上且经过点 的圆
的圆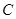 恰好相切于点
恰好相切于点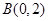 .
.
(1)求椭圆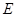 及圆
及圆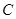 的方程;
的方程;
(2) 在直线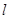 上是否存在一点
上是否存在一点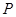 ,使
,使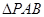 为以
为以 为底边的等腰三角形?若存在,求点
为底边的等腰三角形?若存在,求点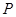 的坐标,否则说明理由.
的坐标,否则说明理由.
(本小题满分12分)
已知 为坐标原点,对于函数
为坐标原点,对于函数 ,称向量
,称向量 为函数
为函数 的伴随向量,同时称函数
的伴随向量,同时称函数 为向量
为向量 的伴随函数.
的伴随函数.
(Ⅰ)设函数 ,试求
,试求 的伴随向量
的伴随向量 的模;
的模;
(Ⅱ)记 的伴随函数为
的伴随函数为 ,求使得关于
,求使得关于 的方程
的方程 在
在 内恒有两个不相等实数解的实数
内恒有两个不相等实数解的实数 的取值范围.
的取值范围.
(本小题满分12分)
如图,抛物线 的顶点为坐标原点
的顶点为坐标原点 ,焦点
,焦点 在
在 轴上,准线
轴上,准线 与圆
与圆 相切.
相切.
(Ⅰ)求抛物线 的方程;
的方程;
(Ⅱ)若点 在抛物线
在抛物线 上,且
上,且 ,求点
,求点 的坐标.
的坐标.
(本小题满分12分)
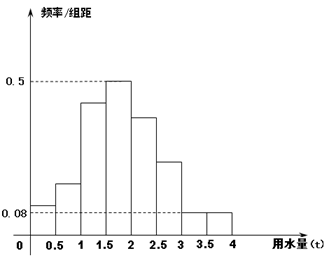
为了解某社区家庭的月均用水量(单位:吨),现从该社区随机抽查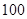 户,获得每户某年的月均用水量,并制作了频率分布表和频率分布直方图(如图).
户,获得每户某年的月均用水量,并制作了频率分布表和频率分布直方图(如图).
(Ⅰ)分别求出频率分布表中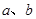 的值,并估计该社区家庭月均用水量不超过
的值,并估计该社区家庭月均用水量不超过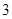 吨的频率;
吨的频率;
(Ⅱ)设 、
、 、
、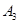 是户月均用水量为
是户月均用水量为 的居民代表,
的居民代表,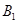 、
、 是户月均用水量为
是户月均用水量为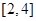 的居民代表. 现从这五位居民代表中任选两人参加水价论证会,请列举出所有不同的选法,并求居民代表
的居民代表. 现从这五位居民代表中任选两人参加水价论证会,请列举出所有不同的选法,并求居民代表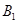 、
、 至少有一人被选中的概率.
至少有一人被选中的概率.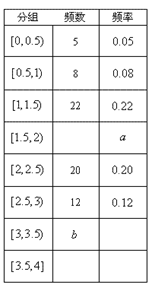
(本小题满分12分)
等差数列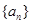 中,
中,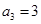 ,
,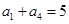 .
.
(Ⅰ)求数列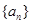 的通项公式;
的通项公式;
(Ⅱ)若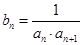 ,求数列
,求数列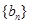 的前
的前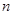 项和
项和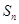 .
.
(本小题满分12分)已知函数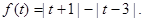
(I)求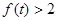 的解集;
的解集;
(II)设a>0,g(x)=ax2-2x+5, 若对任意实数 ,均有
,均有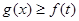 恒成立,求a的取值范围。
恒成立,求a的取值范围。