已知F1、F2是双曲线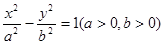 的两焦点,以线段F1F2为边作正三角形MF1F2,若边MF1的中点在双曲线上,则双曲线的离心率是 ( )
的两焦点,以线段F1F2为边作正三角形MF1F2,若边MF1的中点在双曲线上,则双曲线的离心率是 ( )
A. |
B.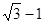 |
C.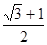 |
D. |
设集合 ,则
,则
| A.(1,2] | B.[0,+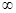 ) ) |
C.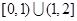 |
D.[0,2] |
一个空间四边形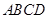 的四条边及对角线
的四条边及对角线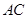 的长均为
的长均为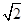 ,二面角
,二面角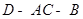 的余弦值为
的余弦值为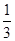 ,则下列论断正确的是
,则下列论断正确的是
A.空间四边形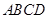 的四个顶点在同一球面上且此球的表面积为 的四个顶点在同一球面上且此球的表面积为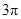 |
B.空间四边形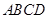 的四个顶点在同一球面上且此球的表面积为 的四个顶点在同一球面上且此球的表面积为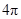 |
C.空间四边形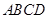 的四个顶点在同一球面上且此球的表面积为 的四个顶点在同一球面上且此球的表面积为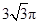 |
D.不存在这样的球使得空间四边形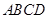 的四个顶点在此球面上 的四个顶点在此球面上 |
设 表示
表示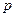 ,
,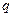 两者中的较小的一个,若函数
两者中的较小的一个,若函数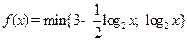 ,则满足
,则满足 的
的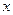 的集合为
的集合为
A.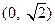 |
B.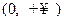 |
C.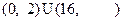 |
D.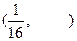 |
已知点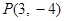 是双曲线
是双曲线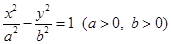 渐近线上的一点,
渐近线上的一点,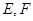 是左、右两个焦点,若
是左、右两个焦点,若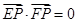 ,则双曲线方程为
,则双曲线方程为
A.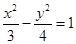 |
B.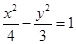 |
C.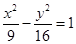 |
D.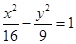 |
在区间[-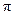 ,
,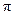 ]内随机取两个数分别记为a,b,则使得函数
]内随机取两个数分别记为a,b,则使得函数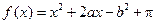 有零点的概率为
有零点的概率为
A.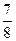 |
B.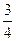 |
C.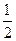 |
D. |