已知数列 满足:
满足: ,
, ,数列
,数列 满足
满足 ,
, .(Ⅰ)求数列
.(Ⅰ)求数列 的通项
的通项 ; (Ⅱ)求证:数列
; (Ⅱ)求证:数列 为等比数列;并求数列
为等比数列;并求数列 的通项公式.
的通项公式.
(本小题满分13分)已知锐角三角形 中,
中,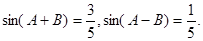
(1)求证: ;
;
(2)设 ,求
,求 边上的高.
边上的高.
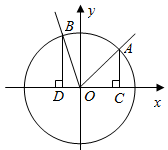
(本小题满分13分)如图,在直角坐标系 中,角
中,角 的顶点是原点,始边与
的顶点是原点,始边与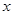 轴正半轴重合.终边交单位圆于点
轴正半轴重合.终边交单位圆于点 ,且
,且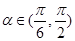 ,将角
,将角 的终边按逆时针方向旋转
的终边按逆时针方向旋转 ,交单位圆于点
,交单位圆于点 ,记
,记 .
.
(1)若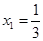 ,求
,求 ;
;
(2)分别过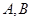 作
作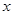 轴的垂线,垂足依次为
轴的垂线,垂足依次为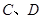 ,记
,记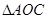 的面积为
的面积为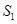 ,
, 的面积为
的面积为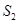 ,若
,若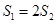 ,求角
,求角 的值.
的值.
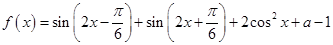 (
(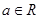 且
且 为常数)
为常数)
(1)求函数的最小正周期;
(2)求函数的单调递减区间;
(3)若 是,
是, 的最小值为-2,求
的最小值为-2,求 的值.
的值.
(本小题满分12分)已知向量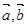 ,满足
,满足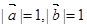 ,
,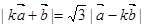 ,
,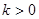 ,
,
(1)用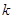 表示
表示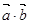 ,并求
,并求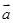 与
与 的夹角
的夹角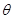 的最大值;
的最大值;
【注:若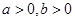 ,则
,则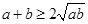 ,当且仅当
,当且仅当 时取等号】
时取等号】
(2)如果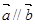 ,求实数
,求实数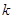 的值.
的值.
(本小题满分12分)已知 .
.
(1) 化简 ;
;
(2) 若 ,求
,求 的值;
的值;
(3) 若 ,且
,且 ,求
,求 的值.
的值.