如图,四棱锥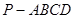 中,底面
中,底面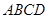 为平行四边形,
为平行四边形,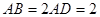 ,
,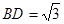 ,
, ⊥底面
⊥底面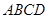 .
.
(1)证明:平面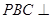 平面
平面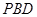 ;
;
(2)若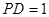 ,求
,求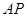 与平面
与平面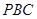 所成角
所成角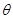 的正弦值.
的正弦值.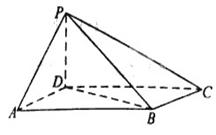
(本小题满分12分)已知直线 ,
,
(1)若直线 过点(3,2)且
过点(3,2)且 ,求直线
,求直线 的方程;
的方程;
(2)若直线 过
过 与直线
与直线 的交点,且
的交点,且 ,求直线
,求直线 的方程.
的方程.
(本小题满分10分)如图甲,⊙ 的直径
的直径 ,圆上两点
,圆上两点 在直径
在直径 的两侧,使
的两侧,使 ,
,  .沿直径
.沿直径 折起,使两个半圆所在的平面互相垂直(如图乙),
折起,使两个半圆所在的平面互相垂直(如图乙), 为
为 的中点.根据图乙解答下列各题:
的中点.根据图乙解答下列各题:
(1)求点 到
到 的距离;
的距离;
(2)在 弧上是否存在一点
弧上是否存在一点 ,使得
,使得 ∥平面
∥平面 ?若存在,试确定点
?若存在,试确定点 的位置;若不存在,请说明理由.
的位置;若不存在,请说明理由.
(本小题满分12分)如图,圆 :
: .
.
(Ⅰ)若圆 与
与 轴相切,求圆
轴相切,求圆 的方程;
的方程;
(Ⅱ)已知 ,圆
,圆 与
与 轴相交于两点
轴相交于两点 (点
(点 在点
在点 的左侧).过点
的左侧).过点 任作一条直线与圆
任作一条直线与圆 :
: 相交于两点
相交于两点 .问:是否存在实数
.问:是否存在实数 ,使得
,使得 ?若存在,求出实数
?若存在,求出实数 的值,若不存在,请说明理由.
的值,若不存在,请说明理由.
(本小题满分12分)如图,在四棱锥P﹣ABCD中,PC⊥底面ABCD,ABCD是直角梯形,AB⊥AD,AB∥CD,AB=2AD=2CD=PC=2.E是PB的中点.
(1)求证:平面EAC⊥平面PBC;
(2)求二面角P—AC—E的余弦值;
(3)求直线PA与平面EAC所成角的正弦值.
(本小题满分12分)已知关于x,y的方程C:  .
.
(1)当m为何值时,方程C表示圆.
(2)若圆C与直线l: x+2y-4=0相交于M,N两点,且MN= ,求m的值.
,求m的值.