已知函数f(x)=ax+x-b的零点x0∈(n, n+1) (n∈Z),其中常数a, b满足2a=3,3b =2,则n的值是 ( )
| A.-2 | B.-1 | C.0 | D.1 |
函数 的单调递增区间为
的单调递增区间为
| A.(0,1) | B. |
C. |
D. |
已知集合A={x|0<log4x<1},B={x|x≤3},则A∩B=
| A.(0,1) | B.(0,3] | C.(1,3) | D.(1,3] |
若点P在曲线y=x3-3x2+(3- )x+
)x+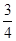 上移动,经过点P的切线的倾斜角为α,则角α的取值范围是( )
上移动,经过点P的切线的倾斜角为α,则角α的取值范围是( )
A.[0,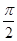 ) ) |
B.[0,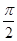 )∪[ )∪[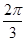 , ,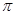 ) ) |
C.[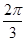 , ,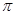 ) ) |
D.[0,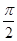 )∪( )∪(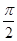 , ,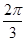 ] ] |
某个命题与正整数有关,若当 时该命题成立,那么可推得当
时该命题成立,那么可推得当 时该命题也成立,现已知当
时该命题也成立,现已知当 时该命题不成立,那么可推得( )
时该命题不成立,那么可推得( )
A.当 时,该命题不成立 时,该命题不成立 |
B.当 时,该命题成立 时,该命题成立 |
C.当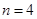 时,该命题成立 时,该命题成立 |
D.当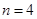 时,该命题不成立 时,该命题不成立 |
在复平面内, 复数1 + i与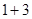 i分别对应向量
i分别对应向量 和
和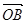 , 其中
, 其中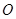 为坐标原点,则
为坐标原点,则 =()
=()
A.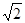 |
B.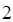 |
C. |
D.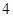 |