若函数f(x)＝ax－x－a(a＞0且a≠1)有两个零点，则实数a的取值范围是( )．
| A．{a|a＞1} | B．{a|a≥2} | C．{a|0＜a＜1} | D．{a|1＜a＜2} |
设函数
的定义域为
，若存在闭区间
，使得函数满足：①在
上是单调函数；②在上的值域是
，则称区间是函数的“和谐区间”．下列结论错误的是（）
A．函数 （ ）存在“和谐区间” |
B．函数 （ ）不存在“和谐区间” |
C．函数  ）存在“和谐区间” |
D．函数 （ ， ）不存在“和谐区间” |
将函数
（
）的图像分别向左平移
（
）个单位，向右平移
（
）个单位，所得到的两个图像都与函数
的图像重合，则
的最小值为（）
A． |
B． |
C． |
D． |
若
展开式中只有第六项的二项式系数最大，则展开式中的常数项是（）
A． |
B． |
C． |
D． |
设向量
，
，则“
∥
”是“
”的（）
| A．充分非必要条件 | B．必要非充分条件 |
| C．充分必要条件 | D．既非充分又非必要条件 |
函数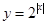
的定义域为
，值域为
，
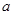变动时，方程
表示的图形可以是（）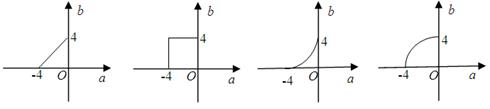
A． B． C．D．