如图所示,在两面墙之间有一个底端在A点的梯子,当它靠在一侧墙上时,梯子的顶端在B点;当它靠在另一侧墙上时,梯子的顶端在D点。已知∠BAC=60°,∠DAE 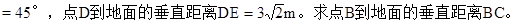
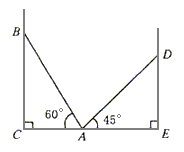
分解因式:(每题5分,共10分)
(1)(m+2n)2-(m-n)2
(2)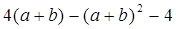
解不等式(组),并把解集在数轴上表示出来。(每小题5分)
⑴ -1<
-1<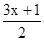
(2)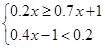
如图,直线y=x-1和抛物线y=x2+bx+c都经过点A(1,0),B(3,2).
(1)求抛物线的解析式;
(2)求不等式x2+bx+c<x-1的解集(直接写出答案)
(3)设直线AB交抛物线对称轴与点D,请在对称轴上求一点P(D点除外),使△PBD为等腰三角形.(直接写出点P的坐标,不写过程)
如图,矩形ABCD,AB=6cm,AD=2cm,点P以2cm/s的速度从顶点A出发沿折线A-B-C向点C运动,同时点Q以lcm/s的速度从顶点C出发向点D运动,当其中一个动点到达末端停止运动时,另一点也停止运动.
(1)问两动点运动几秒,使四边形PBCQ的面积是矩形ABCD面积的 ;
;
(2)问两动点经过多长时间使得点P与点Q之间的距离为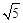 ?若存在,求出运动所需的时间;若不存在,请说明理由.
?若存在,求出运动所需的时间;若不存在,请说明理由.
已如图,反比例函数 y=的图象与一次函数y=mx+b的图象交于两点A(1,3) ,B(n,-1). 
(1)求反比例函数与一次函数的函数关系式;
(2)根据图象,直接回答:当x取何值时,一次函数的值大于反比例函数的值;答:
(3) 连接AO、BO,求△ABO的面积;