“知识改变命运，科技繁荣祖国”．我区中小学每年都要举办一届科技比赛．下图为我区某校2010年参加科技比赛（包括电子百拼、航模、机器人、建模四个类别）的参赛人数统计图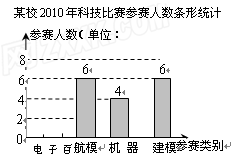
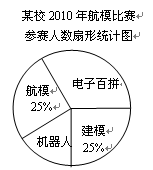
（1）该校参加机器人、建模比赛的人数分别是 人和 人；
（2）该校参加科技比赛的总人数是 人，电子百拼所在扇形的圆心角的度数是 °，并把条形统计图补充完整；
（3）从全区中小学参
加科技比赛选手中随机抽取80人，其中有32人获奖. 今年我区中小学参加科技比赛人数共有2485人，请你估算今年参加科技比赛的获奖人数约是多少人?
已知：关于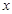
的一元二次方程
．
（1）求实数k的取值范围；
（2）设上述方程的两个实数根分别为x1、x2，求：当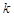
取哪些整数时，x1、x2均为整数；
（3）设上述方程的两个实数根分别为x1、x2，若
，求k的值．
某水果专卖店销售樱桃，其进价为每千克40元，按每千克60元出售，平均每天可售出100千克，后来经过市场调查发现，单价每千克降低1元，则平均每天的销售可增加10千克，若该专卖店销售这种樱桃要想平均每天获利2240元，请回答：
（1）每千克樱桃应降价多少元？
（2）在平均每天获利不变的情况下，为尽可能让利于顾客，赢得市场，该店应按原售价的几折出售？
已知关于
的一元二次方程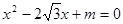
有两个不相等的实数根．
（1）求实数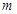
的取值范围；
（2）在（1）的条件下，化简：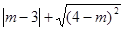
．
如图，圆内接四边形ABDC，AB是⊙O的直径，OD⊥BC于E．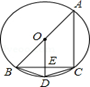
（1）求证：∠BCD=∠CBD；
（2）若BE=4，AC=6，求DE的长．
已知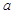
是方程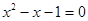
的一个根，求
的值．