设 、
、 为两个不同的平面,n、m为两条不同的直线,且n
为两个不同的平面,n、m为两条不同的直线,且n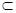
 ,m
,m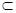
 ,有如下的两个命题:①若
,有如下的两个命题:①若 ∥
∥ ,则n∥m;②若n⊥m,则
,则n∥m;②若n⊥m,则 ⊥
⊥ .那么 ( )
.那么 ( )
| A.①是真命题,②是假命题 | B.①是假命题,②是真命题 |
| C.①②都是真命题 | D.①②都是假命题 |
命题:“若 ,则
,则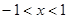 ”的逆否命题是()
”的逆否命题是()
A.若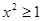 ,则 ,则 |
B.若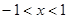 ,则 ,则 |
C.若 ,则 ,则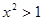 |
D.若 ,则 ,则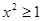 |
设全集U=R,A= ,则右图中阴
,则右图中阴
影部分表示的集合为 ( )
A. |
B. |
C.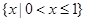 |
D.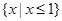 |
已知x2+y 2 =" 1" ,若x + y -k ≥0对符合条件一切x、y都成立,则实数k的最大值为()
A. |
B.0 | C.- |
D.1 |
现安排甲、乙、丙、丁、戊5名同学参加上海世博会志愿者服务活动,每人从事翻译、导游、礼仪、司机四项工作之一,每项工作至少有一人参加.甲、乙不会开车但能从事其他三项工作,丙、丁、戊都能胜任四项工作,则不同安排方案的种数是( )
| A.152 | B.126 | C.90 | D.54 |
.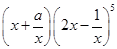 的展开式中各项系数的和为2,则该展开式中常数项为()
的展开式中各项系数的和为2,则该展开式中常数项为()
| A.-40 | B.-20 | C.20 | D.40 |