已知函数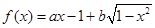 ,其中
,其中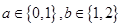 ,则使得
,则使得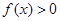 在
在 上有解的概率为( )
上有解的概率为( )
A.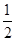 |
B. |
C.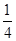 |
D. |
已知直线mx+4y-2=0与2x-5y+n=0互相垂直,垂足为(1,p),则m-n+p为( )
| A.24 | B.20 | C.0 | D.-4 |
已知A(-1,1),B(3,-5),则线段AB的垂直平分线方程是( )
| A.3x+2y-2="0" | B.2x+3y+2=0 |
| C.3x-2y+8="0" | D.2x-3y-8=0 |
x轴上任一点到定点(0,2)、(1,1)距离之和的最小值是( )
A. |
B. |
C. |
D. |
知A(3,-1)、B(5,-2),点P在直线x+y=0上,若使|PA|+|PB|取最小值,则点P的坐标是( )
| A.(1,-1) | B.(-1,1) | C. |
D.(-2,2) |
两直线ax+by+m=0与ax+by+n=0的距离是( )
| A.|m-n| | B. |
C. |
D. |