2011年3月10日，云南省发生了5.8级地震，我区某中学开展了“情系云南，大爱无疆”爱心捐款活动．团干部对九（1）班的捐款情况进行了统计，并把统计的结果制作了一个不完全的频数分布直方图和扇形统计图．已知学生捐款最少的是5元，最多的不足25元．
请补全频数分布直方图
九（1）班学生捐款的中位数所在的组别范围是＿＿＿＿；
九（1）班学生小明捐款24元，班主任拟在捐款最多的20－25元这组同学中随机选取一人代表班级在学校组织的爱心活动大会上发言，小明同学被选中的概率是＿＿＿＿．
解分式方程：
已知多边形ABDEC是由边长为2的等边三角形ABC和正方形BDEC组成，一圆过A、D、E三点，求该圆半径的长．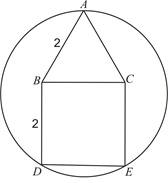
如图，已知⊙O的半径为8cm，点A为半径OB的延长线上一点，射线AC切⊙O于点C，BC的弧长为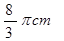
，求线段AB的长。
如图，在△ABC中，∠C＝90°，∠A、∠B的平分线交于点D，DE⊥BC于点E，DF⊥AC于点F，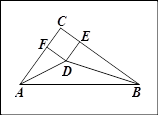
（1）求证：四边形CFDE是正方形
（2）若AC＝3，BC＝4，求△ABC的内切圆半径.
为了降低能源消耗，减少环境污染，国务院办公厅下发了“关于限制生产销售使用塑料购物袋的通知”，并从2008年6月1日起正式实施．某中学八年级共有400名学生。学校为了增强学生的环保意识，在本年级进行了一次环保知识测验．为了了解这次测验的成绩状况，从中抽取了50名学生的成绩，将所得数据整理后，画出频数分布直方图如图所示．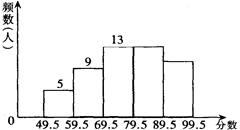
(1)第五个小组的频数和频率各是多少?
(2) 这50名学生的成绩的中位数在哪一组?
(3)这次测验中，八年级全体学生成绩在59.5～69.5中的人数约是多少?