（本题8分）如图，在直角坐标系中，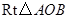
的两条直角边
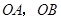分别在
轴的负半轴，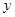
轴的负半轴上，且
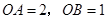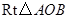．将绕点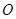
按顺时针方向旋转
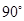，再把所得的像沿轴正方向平移1个单位，得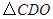
．
（1）写出点
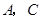的坐标；（2）求点
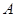和点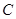
之间的距离．
如图所示，直线AB, CD相交于点O, P是直线CD上一点。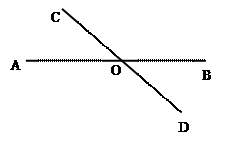
①过点P画直线AB的垂线段PE;
②过点P画直线CD的垂线，与直线AB相交于F点；
③说明线段PE, PO, FO三者的大小关系，其依据是什么？
如图，零件的外径为16cm，要求它的壁厚x，需要先求出内径AB，现用一个交叉钳(AD与BC相等)去量，若测得OA
︰OD=OB︰OC=3︰1，CD＝5cm，你能求零件的壁厚x吗？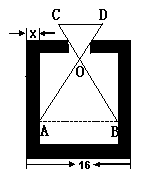
如图，点D、E分别在AC、BC上，如果测得CD＝20m，CE＝40m，AD=100m，BE
=20m，DE=45m,求A、B两地间的距离。
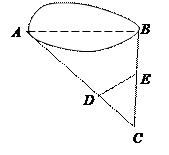
如图，有一路灯杆AB（底部B不能直接到达），在灯光下，小明在点D处测得自己的影长DF＝3m，沿BD方向到达点F处再测
得自己得影长FG＝4m，如果小明得身高为1.6m，求路灯杆AB的高度。
如图，△ABC中， EF∥BC，FD∥AB，AE＝18，BE＝12，CD＝14，求线段EF的长．