已知某正数的两个平方根分别是a+3和2a-15,b的立方根是-2，求3a+b的算术平方根.
（1）计算：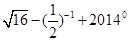
；（2）求
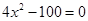中x的值．
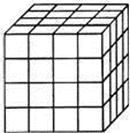
将一个正方体表面全部涂上颜色
把正方体的棱三等分，然后沿等分线把正方体切开，得到27个小正方体，我们把仅有i个面涂色的小正方体的个数记为
，例如：通过观察我们可以发现仅有3个面涂色的小正方体个数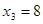
，仅有2个面涂色的小正方体个数
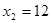，仅有1个面涂色的小正方体个数
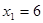，6个面均不涂色的小正方体个数
；
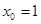（1）如果把正方体的棱四等分，同样沿等分线把正方体切开，得到64个小正方体，那么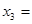
________，
_______，
_______，
_________；
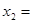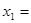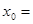（2）如果把正方体的棱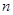
等分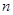（大于3），然后沿等分线把正方体切开，得到
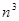个小正方体，且满足
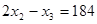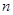，请求出的值.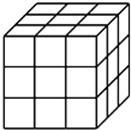
如图是计算机程序计算图.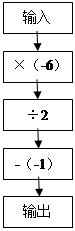
（1）若开始输入为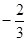
，请你根据程序列出算式并计算出输出结果；
（2）若最后输出为-4，请你根据程序列出算式并计算出输入数字.
规定一种新运算a⊙b=a2 -2b.
（1）求（-1）⊙2的值；
（2）若2⊙
=6，求
的值。
，其中
．