如图所示,在倾角为θ的光滑斜面上垂直纸面放置一根长为L、质量为m的直导体棒ab,通以方向向里的电流,电流强度为I,重力加速度为g,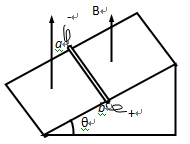
若加竖直向上的匀强磁场,使导体棒静止在斜面上,求所加磁场的磁感应强度B的大小;
若匀强磁场的大小、方向都可以改变,要使导体棒能静止在斜面上,求所加磁场的磁感应强度B的最小值和所对应方向。
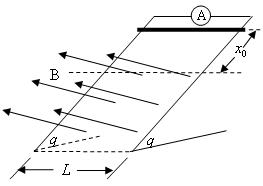
如图所示,两足够长的光滑平行固定金属导轨与水平面的夹角为 ,匀强磁场与导轨平面垂直。一质量为m、有效电阻为R的导体棒在距磁场上边界
,匀强磁场与导轨平面垂直。一质量为m、有效电阻为R的导体棒在距磁场上边界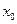 处静止释放。导体棒进入磁场后,流经理想电流表的电流逐渐减小,最终稳定为I。整个运动过程中,导体棒与导轨接触良好,且始终保持水平,不计导轨的电阻,重力加速度为
处静止释放。导体棒进入磁场后,流经理想电流表的电流逐渐减小,最终稳定为I。整个运动过程中,导体棒与导轨接触良好,且始终保持水平,不计导轨的电阻,重力加速度为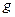 。求:
。求:
(1)磁感应强度的大小B;
(2)电流稳定后,导体棒运动速度的大小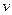 ;
;
(3)流经电流表电流的最大值 。
。
北京奥运会的开闭幕式给我们留下了深刻的印象。在闭幕式演出中出现了一种新型弹跳鞋叫弹跳跷,主要是由后面的弹簧(弓)和铝件组成。绑在脚上,能够一步行走二到三米的距离,弹跳高度达到一至两米,是青年中新兴的一种体育运动。一名质量m=60kg的学生穿着这种鞋从距地面H=1.8m高处由静止落下,与水平地面撞击后反弹上升的最大高度h=1.25m。忽略空气阻力,取重力加速度g=10m/s2,求:
⑴学生与地面撞击过程中损失的机械能;
⑵学生与地面撞击过程中速度改变量的大小和方向。
如图所示,实线是一列简谐横波在t1=0时刻的波形图,虚线为t2=0.5s时的波形图,已知0<t2-t1<T,t1=0时,x=2m处的质点A正向y轴正方向振动。求:
(1)质点A的振动周期为多少;
(2)波的传播速度大小和方向;
(3)从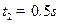 时刻计时,写出
时刻计时,写出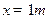 处质点的振动方程。
处质点的振动方程。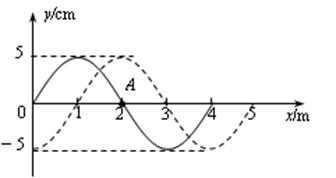
一种油的密度为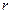 ,摩尔质量为
,摩尔质量为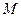 .取体积为
.取体积为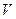 的油慢慢滴出,可滴
的油慢慢滴出,可滴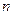 滴.将其中一滴滴在广阔水面上,形成面积为
滴.将其中一滴滴在广阔水面上,形成面积为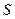 的单分子油膜。由此可求出:
的单分子油膜。由此可求出:
(1)该油分子的直径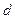 ;
;
(2)阿伏加德罗常数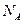 ;
;
(3)其中一滴油滴含有的分子数 。
。
 是竖直平面内的四分之一圆弧轨道,在下端B与水平直轨道相切,如图所示.一小球自A点起由静止开始沿轨道下滑.已知圆轨道半径为R,小球的质量为m,不计各处摩擦.求:
是竖直平面内的四分之一圆弧轨道,在下端B与水平直轨道相切,如图所示.一小球自A点起由静止开始沿轨道下滑.已知圆轨道半径为R,小球的质量为m,不计各处摩擦.求:
(1)小球运动到B点时的动能
(2)小球经过圆弧轨道的B点和水平轨道的C点时,所受轨道支持力FB、FC各是多大?