某单位欲招聘一名员工，现有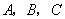
三人竞聘该职位，他们的笔试成绩和口试成绩（单位：分）分别用两种方式进行了统计，如表一和图一
请将表一和图一中的空缺部分补充完整；
竞聘的最后一个程序是由该单位的
名职工进行投票，三位竞聘者的得票情
况如图二（没有弃权票，每名职工只能推荐一个），请计算每人的得票数；若每票计
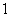分，该单位将笔试、口试、得票三项测试得分按
的比例确定
个人成绩，请计算三位竞聘者的最后成绩，并根据成绩判断谁能竞聘成功．
实数a、b在数轴上的位置如图，化简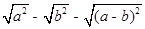
如图，矩形OABC在平面直角坐标系xoy中，点A在x轴的正半轴上，点C在y轴的正半轴上，OA=4,OC=3，若抛物线的顶点在BC边上，且抛物线经过O、A两点，直线AC交抛物线于点D。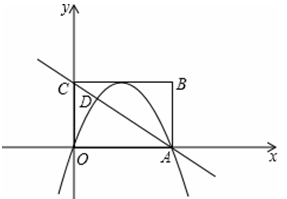
（1）求抛物线的解析式；
（2）求点D的坐标；
（3）若点M在抛物线上，点N在x轴上，是否存在以点A、D、M、N为顶点的四边形是平行四边形？若存在，求出点N的坐标；若不存在，请说明理由。
在矩形ABCD中，点E在BC边上，过E作EF⊥AC于F，G为线段AE的中点，连接BF、FG、GB．设
＝k．
（1）证明：△BGF是等腰三角形；
（2）当k为何值时，△BGF是等边三角形？并说明理由。
（3）我们知道：在一个三角形中，等边所对的角相等；反过来，等角所对的边也相等．事实上，在一个三角形中，较大的边所对的角也较大；反之也成立．利用上述结论，探究：当△BGF分别为锐角、直角、钝角三角形时，k的取值范围．
直线y=x+b与x轴交于点C（4,0），与
轴交于点B，并与双曲线y=
（x＜0）交于点A（－1，n）。
（1）求直线与双曲线的解析式。
（2）连接OA，求∠OAB的正弦值。
（3）若点D在x轴的正半轴上，是否存在以点D、C、B构成的三角形与△OAB相似？若存在求出D点的坐标，若不存在，请说明理由。
有一人患了流感，经过两轮传染后共有64人患了流感．
（1）求每轮传染中平均一个人传染了几个人？
（2）如果不及时控制，第三轮将又有多少人被传染？