下面四个命题中正确的是:( )
A.“直线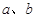 不相交”是“直线 不相交”是“直线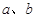 为异面直线”的充分非必要条件 为异面直线”的充分非必要条件 |
B.“ 平面 平面 ”是“直线 ”是“直线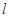 垂直于平面 垂直于平面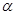 内无数条直线”的充要条件 内无数条直线”的充要条件 |
C.“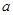 垂直于 垂直于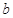 在平面 在平面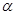 内的射影”是“直线 内的射影”是“直线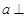 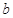 ”的充分非必要条件 ”的充分非必要条件 |
D.“直线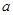 平行于平面 平行于平面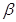 内的一条直线”是“直线 内的一条直线”是“直线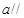 平面 平面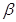 ”的必要非充分条件 ”的必要非充分条件 |
求证: +
+ >
> .
.
证明:因为 +
+ 和
和 都是正数,
都是正数,
所以为了证明 +
+ >
> ,
,
只需证明( +
+ )2>(
)2>( )2,
)2,
展开得5+2 >5,即2
>5,即2 >0,显然成立,
>0,显然成立,
所以不等式 +
+ >
> .上述证明过程应用了()
.上述证明过程应用了()
| A.综合法 |
| B.分析法 |
| C.综合法、分析法混合 |
| D.间接证法 |
要证 ,只需证
,只需证 +1,即需证
+1,即需证 ,即需证
,即需证 ,即证35>11,因为35>11显然成立,所以原不等式成立.以上证明运用了()
,即证35>11,因为35>11显然成立,所以原不等式成立.以上证明运用了()
| A.比较法 | B.综合法 | C.分析法 | D.反证法 |
下面叙述正确的是()
| A.综合法、分析法是直接证明的方法 |
| B.综合法是直接证法、分析法是间接证法 |
| C.综合法、分析法所用语气都是肯定的 |
| D.综合法、分析法所用语气都是假定的 |
“执果索因”是下列哪种证明方法的特点()
| A.数学归纳法 | B.反证法 | C.分析法 | D.综合法 |
数学中的综合法是()
| A.由结果追溯到产生原因的思维方法 |
| B.由原因推导到结果的思维方法 |
| C.由反例说明结果不成立的思维方法 |
| D.由特例推导到一般的思维方法 |