如右图所示，细绳长l，吊一个质量为m的铁球，绳受到大小为2mg的拉力就会断裂，绳的上端系一质量不计的环，环套在光滑水平杆上．起初环带着球一起以速度
向右运动，在A处环被挡住而停下的瞬间，绳子所受拉力为多少？在以后的运动过程中，球是先碰墙还是先碰地？第一次的碰撞点离B点的距离是多少？（已知A处离墙的水平距离为l，球离地的高度h=2l）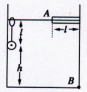
一辆汽车以72km/h的速度匀速行驶，现因故障紧急刹车并最终停止运动．已知汽车刹车过程加速度的大小为5m/s2，试求：
（1）从开始刹车经过3s时的瞬时速度是多少？
（2）从开始刹车经过5s，汽车通过的距离是多少？
（3）从开始刹车经过30m所用的时间是多少？
汽车在平直公路上以10m/s的速度做匀速直线运动，发现前面有情况而刹车，若获得的加速度大小为2m/s2,则经过6s汽车的速度有多大？
一列长50m的队伍，以1．5m/s速度经过一座全长为100m的桥，当队伍的第一个人踏上桥到队尾最后一人离开桥时，总共需要的时间是多少？
一个质量m= 6kg的物体，初速度v0=2m/s,受到水平方向的拉力F=10N，如图所示，在水平地面上移动的距离L=2m，物体与地面间的滑动摩擦力f= 4N，求：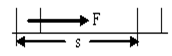
（1）拉力和摩擦力对物体所做的功；
（2）合外力对物体所做的功；
（3）在此过程中物体获得的速度大小。
如图，质量m=50kg的跳水运动员从距水面高h=10m的跳台上以v0=5m/s的速度斜向上起跳，最终落入水中。若忽略运动员的身高。取g=10m/s2。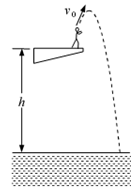
求：（1）运动员在跳台上时的重力势能（以水面为参考平面）；
（2）运动员起跳时的动能；
（3）运动员入水时的速度大小。