设集合 ,则满足
,则满足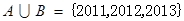 的集合B的个数为( )
的集合B的个数为( )
| A.1 | B.3 | C.4 | D.8 |
用反证法证明命题:“三角形的内角中至少有一个不大于60度”时,反设正确的是()
| A.假设三内角都不大于60度 |
| B.假设三内角都大于60度 |
| C.假设三内角至多有一个大于60度 |
| D.假设三内角至多有两个大于60度 |
下面是调查某地区男女中学生喜欢理科的等高条形图,阴影部分表示喜欢理科的百分比,从图可以看出()
| A.性别与喜欢理科无关 |
| B.女生中喜欢理科的比为80% |
| C.男生比女生喜欢理科的可能性大些 |
| D.男生不喜欢理科的比为60% |
有一段演绎推理:“直线平行于平面,则这条直线平行于平面内所有直线;已知直线 平面
平面 ,直线
,直线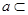 平面
平面 ,直线
,直线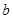 ∥平面
∥平面 ,则直线
,则直线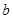 ∥直线
∥直线 ”的结论是错误的,这是因为()
”的结论是错误的,这是因为()
| A.大前提错误 | B.小前提错误 |
| C.推理形式错误 | D.非以上错误 |
如果复数 ,满足条件
,满足条件 ,那么实数a的取值范围是()
,那么实数a的取值范围是()
A.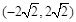 |
B.(-2,2) |
| C.(-1,1) | D.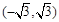 |
复平面内,复数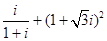 对应的点位于()
对应的点位于()
| A.第一象限 | B.第二象限 | C.第三象限 | D.第四象限 |