一个半径r=0.10m的闭合导体圆环，圆环单位长度的电阻R0=1.0×10-2W×m-1。如图19甲所示，圆环所在区域存在着匀强磁场，磁场方向垂直圆环所在平面向外，磁感应强度大小随时间变化情况如图19乙所示。（1）分别求在0~0.3 s和0.3 s~0.5s 时间内圆环中感应电动势的大小；（2）分别求在0~0.3 s和0.3 s~0.5s 时间内圆环中感应电流的大小，并在图19丙中画出圆环中感应电流随时间变化的i-t图象（以线圈中逆时针电流为正，至少画出两个周期）；（3）求在0~10s内圆环中产生的焦耳热。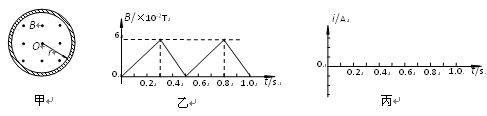
发电机转子是100匝边长为20cm的正方形线圈，将它置于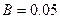
T的匀强磁场中，绕着垂直于磁场方向的轴以
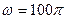rad/s的角速度转动，转动开始时线圈平面与磁场方向垂直，已知线圈的电阻为2
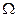，外电路的电阻为8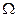，试求：
（1）交变电流的瞬时表达式；
（2）如保持转子匀速转动，外力每分钟需要对转子所做的功；
（3）从计时开始，线圈转过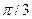
的过程中，通过外电阻的电量。
一台交流发电机的输出电压为250V，输出功率为100kW，向远处输电用的输电线总电阻为8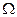
。为了使输电线上损耗的功率不超过输送总功率的5%，且用户端刚好能得到220V交变电压，求供电端的升压变压器和用户端的降压变压器的变压比应分别是多少？
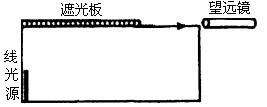
如图，置于空气中的一不透明容器中盛满某种透明液体。容器底部靠近器壁处有一竖直放置的6.0cm长的线光源。靠近线光源一侧的液面上盖有一遮光板，另一侧有一水平放置的与液面等高的望远镜，用来观察线光源。开始时通过望远镜不能看到线光源的任何一部分。将线光源沿容器底向望远镜一侧平移至某处时，通过望远镜刚好可能看到线光源底端。再将线光源沿同一方向移动8.0cm，刚好可以看到其顶端。求此液体的折射率
。
图中所示实线和虚线分别表示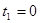
和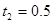
s时的简谐横波的图象，则波速为多大？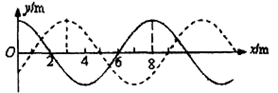
如图（a）所示，两块足够大的平行金属板竖直放置，板间加有匀强电场和磁场，电场和磁场的大小随时间按图（b）和图（c）所示的规律变化（规定垂直于纸面向外为磁感应强度的正方向）。在t=0时，由负极板内侧释放一初速度为零的带负电粒子，粒子的重力不计。在t=37t0/12时，带电粒子被正极板吸收。已知电场强度E0、粒子的比荷q/m以及t0。而磁感应强度B1、B2(均未知)的比值为1﹕3，在t0～2t0时间内，粒子在磁场中做匀速圆周运动的周期为t0。求：
（1）当带电粒子离负极板的距离S0="q" E0t02/2m时，粒子在两极板间运动的时间；
（2）两平行板间的距离d 。
