如图,在△ABC中,D是BC边上的一点,E是AD的中点,过A点作BC的平行线交CE的延长线于F,且AF=BD,连接BF。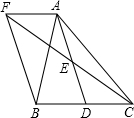
(1)求证:D是BC的中点
(2)如果AB=AC,试判断四边形AFBD的形状,并证明你的结论。
如图所示,在Rt△ABC中,AD平分∠BAC,交BC于D,CH⊥AB于H,交AD于F,DE⊥AB垂足为E,求证:四边形CFDE是菱形。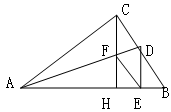
一个多边形的每个内角都相等,都等于150°,求这个多边形的边数?
一个同学在进行多边形的内角和计算时,求的内角和为2750°,当发现错了之后,重新检查,发现少加了一个内角,问这个内角的度数是多少?求这个多边形的边数。
如果一个多边形的每一个外角都小于45°,求这样多边形的边数的最小值。