如图，平面直角坐标系中，点A坐标（2,0），点B是y轴上的一个动点，连结AB，取AB中点M，将线段AM绕着点A顺时针方向旋转90°得到线段AN，连结ON、BN，ON与AB所在直线交于点P，设点B的坐标为（0，t）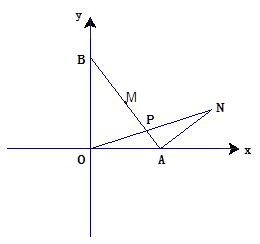
（1）当t>0时，用t的代数式表示点N的坐标；
（2）设△OBN的面积为S，求S关于t的函数关系式；
（3）是否存在点B，使得△ABN与△ANP相似？若存在，求出符合条件的点B的坐标，若不存在，请说明理由。
已知：如图，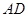
∥
，
。
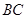求证：
。
解不等式组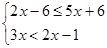
，并将它的解集在数轴上表示出来。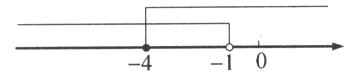
解不等式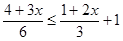
，并写出它的非正整数解。
解方程组：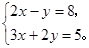
如图，矩形OABC的边OA在x轴正半轴上，边OC在y轴正半轴上，B点的坐标为(1，3)．矩形O'A'BC'是矩形OABC绕B点逆时针旋转得到的．O'点恰好在x轴的正半轴上， O'C'交AB于点D.
(1)求点O'的坐标，并判断△O'DB的形状（要说明理由）(4分)
(2)求边C'O'所在直线的解析式．(4分)
(3)延长BA到M使AM=1，在(2)中求得的直线上是否存在点P，使得ΔPOM是以线段OM为直角边的直角三角形?若存在，请直接写出P点的坐标；若不存在，请说明理由．(2分)