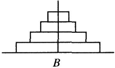
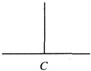
如下图,汉诺塔问题是指有3根杆子A,B,C.B杆上有若干碟子,把所有碟子从B杆移到A杆上,每次只能移动一个碟子,大的碟子不能叠在小的碟子上面.把B杆上的4个碟子全部移到A杆上,最少需要移动( )次. ( )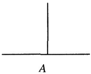
A.12 B.15 C.17 D.19
若 则
则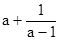 的最小值是()
的最小值是()
| A.2 | B.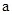 |
C.3 | D. |
下面几种推理是类比推理的是()
A.两条直线平行,同旁内角互补,如果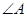 和 和 是两条平行直线的同旁内角,则 是两条平行直线的同旁内角,则  |
| B.由平面向量的运算性质,推测空间向量的运算性质 |
| C.某校高二级有20个班,1班有51位团员,2班有53位团员,3班有52位团员,由此可以推测各班都超过50位团员,; |
D.一切偶数都能被2整除,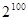 是偶数,所以 是偶数,所以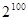 能被2整除 能被2整除 |
在回归直线方程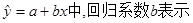 ()
()
A.当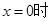 , ,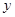 的平均值 的平均值 |
B.当 变动一个单位时, 变动一个单位时,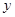 的实际变动量 的实际变动量 |
C.当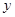 变动一个单位时, 变动一个单位时, 的平均变动量 的平均变动量 |
D.当 变动一个单位时, 变动一个单位时,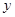 的平均变动量 的平均变动量 |
数列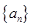 中
中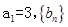 等差数列且
等差数列且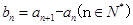 ,若
,若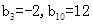 则
则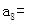
| A.0 | B.3 | C.8 | D.11 |
在△ABC中,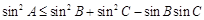 ,则A的取值范围是
,则A的取值范围是
A.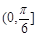 |
B.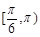 |
C.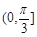 |
D.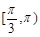 |