已知:如图1,在Rt⊿ACB中,∠C=90°,AC=4cm,BC=3cm,点P由点B出发沿BA方向向点A匀速运动,速度为1cm/s;点Q由点A出发沿AC方向向点C匀速运动,速度为2cm/s;连接PQ.若设运动的时间为t(s)(0<t<2).解答下列问题:
①.当t为何值时,PQ∥BC?
②.设⊿AQP的面积为y(cm
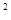 ),求y与t之间的函数关系式;
),求y与t之间的函数关系式;③.是否存在某一时刻t,使线段PQ恰好把Rt⊿ACB的周长和面积同时平分?若存在,求出此时t的值;若不存在,说明理由;
④.如图2,连接PC,并把⊿PQC沿QC翻折,得到四边形PQ
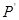 C,那么是否存在某时刻t,使四边形PQ
C,那么是否存在某时刻t,使四边形PQ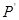 C为菱形?若存在,求出此时菱形的边长;若不存在,说明理由。
C为菱形?若存在,求出此时菱形的边长;若不存在,说明理由。
如图,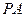 为
为 的切线,
的切线,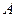 为切点,
为切点,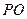 交
交 于点
于点 ,求
,求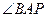 的度数.
的度数.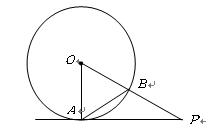
已知方程组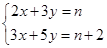 的解x、y的和为12,求n的值.
的解x、y的和为12,求n的值.
如图①,一条笔直的公路上有A、B、C 三地 ,B、C 两地相距150千米,甲、乙两辆汽车分别从
,B、C 两地相距150千米,甲、乙两辆汽车分别从
B、C两地同时出发,沿公路匀速相向而行,分别驶往C、B 两地.甲、乙两车到A地的距离 、
、 (千米)与行驶时间x(时)的关系如图②所示.
(千米)与行驶时间x(时)的关系如图②所示.
根据图象②进行以下探究:
求图中②M点的坐标,并解释该点的实际意义.
在图②中补全甲车的函数图象,求甲车到A地的距离
 与行驶时间x的函数关系式.
与行驶时间x的函数关系式.A地设有指挥中心,指挥中心及两车都配有对讲机,两部对讲机在15千米之内(含15千米)时能够互相通话,求两车可以同时与指挥中心用对讲机通话的时间.
在平面直角坐标系中,一次函数的图象与坐标轴围成的三 角形,叫做此一次函数的坐标三角形.例如,图中的一次函数的图象与x,y轴分别交于点A,B,则△OAB为此函数的坐标三角形.
角形,叫做此一次函数的坐标三角形.例如,图中的一次函数的图象与x,y轴分别交于点A,B,则△OAB为此函数的坐标三角形.
求函数y=
 x+3的坐标三角形的三条边长;
x+3的坐标三角形的三条边长;若函数y=
 x+b(b为常数)的坐标三角形周长为16,
x+b(b为常数)的坐标三角形周长为16,
求此三角形面积.
我国是世界上严重缺水的国家之一.为了倡导“节约用水从我做起”,小刚在他所在班的50名同学中,随机调查了10名同学家庭中一年的月均用水量(单位:t),并将调查结果绘成了如下的条形统计图求这10个样本数据的平均数、众数和中位数;
根据样本数据,估计小刚所在班50名同学家庭中月均用水量不超过7 t的约有多少户.