如图所示,一质量为m的氢气球用细绳拴在地面上,地面上空风速水平且恒为 ,球静止时绳与水平方向夹角为α。某时刻绳突然断裂,氢气球飞走。己知氢气球.在空气中运动时所受到的阻力f正比于其相对空气速度v,可以表示为
,球静止时绳与水平方向夹角为α。某时刻绳突然断裂,氢气球飞走。己知氢气球.在空气中运动时所受到的阻力f正比于其相对空气速度v,可以表示为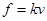 (k为已知的常数)。则
(k为已知的常数)。则
(1)氢气球受到的浮力为多大?
2)绳断裂瞬间,氢气球加速度为多大?
(3)一段时间后氢气球在空中嫩匀速直线运动,其水平方向上的速度与风速 相等,求此时气球速度大小(设空气密度不发生变化,重力加速度为g)。
相等,求此时气球速度大小(设空气密度不发生变化,重力加速度为g)。
如图所示,长度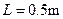 的轻质细杆OP,P端有一质量
的轻质细杆OP,P端有一质量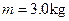 的小球,小球在最低点获得V=
的小球,小球在最低点获得V=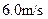 的速度后以O点为圆心在竖直平面内做圆周运动,不计细杆在O的摩擦和空气阻力。求:(1)小球通过最高点时的速率(2)小球通过最高点时杆OP受到小球的力的大小和方向。(
的速度后以O点为圆心在竖直平面内做圆周运动,不计细杆在O的摩擦和空气阻力。求:(1)小球通过最高点时的速率(2)小球通过最高点时杆OP受到小球的力的大小和方向。(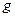 取
取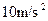 )
)
一颗绕地球运转的卫星,距地面高度为 .已知地球半径为R,地面重力加速度为
.已知地球半径为R,地面重力加速度为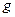 .求这颗卫星运转的线速度大小和周期分别是多少?
.求这颗卫星运转的线速度大小和周期分别是多少?
用200N的拉力将地面上一个质量为10kg的物体加速提升10m至A点,空气阻力忽略不计。g取 。求:(1)这一过程中重力对物体所做的功。(2)这一过程中拉力对物体所做的功。(3)物体在A点具有的动能。
。求:(1)这一过程中重力对物体所做的功。(2)这一过程中拉力对物体所做的功。(3)物体在A点具有的动能。
将小球从距地面0.8m高处以 的速度水平抛出, g取
的速度水平抛出, g取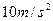 。求小球在空中运动的时间和落地时速度的大小.
。求小球在空中运动的时间和落地时速度的大小.
某压力锅结 构如图所示。盖好密封锅盖,将压力阀套在出气孔上,给压力锅加热,当锅内气体压强达到一定值时,气体就把压力阀顶起。假定在压力阀被顶起时,停止加热。
构如图所示。盖好密封锅盖,将压力阀套在出气孔上,给压力锅加热,当锅内气体压强达到一定值时,气体就把压力阀顶起。假定在压力阀被顶起时,停止加热。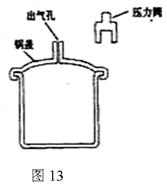
(1)若此时锅内气体的体积为V,摩尔体积为V0,阿伏加德罗常数为NA,写出锅内气体分子数的估算表达式。
(2)假定在一次放气过程中,锅内气体对压力阀及外界做功1 J,并向外界释放了2 J的热量。锅内原有气体的内能如何变化?变化了多少?
(3)已知大气压强P随海拔高度H的变化满足P=P0(1-αH),其中常数α>0。结合气体定律定性分析在不同的海拔高度使用压力锅,当压力阀被顶起时锅内气体的温度有何不同。