如图所示，直角坐标系xOy位于竖直平面内，在水平的x轴下方存在匀强磁场和匀强电场，磁场的磁感应为B，方向垂直xOy平瑶向里，电场线平行于y轴。一质量为m．电荷量为q的带正电的小球，从y轴上的A点水平向右抛出，经x轴上的M点进入电场和磁场，恰能做匀速圆周运动，从x轴上的N点第一次离开电场和磁场，MN之间的距离为L，小球过M点时的速度方向与x轴的方向夹角为
。不计空气阻力，重力加速度为g，求
（1）电场强度E的大小和方向；
（2）小球从A点抛出时初速度
的大小；
（3）A点到x轴的高度h。
如图所示,劲度系数为k2的轻质弹簧,竖直放在桌面上,上面压一质量为m的物体,另一劲度系数为k1的轻质弹簧竖直地放在物体上面,其下端与物块上表面连接在一起,要想物体在静止时,下面弹簧承受物重的2/3,应将上面弹簧持上端A竖直向上提高多大的距离?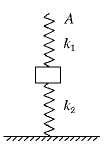
如图所示,为一轻质弹簧的长度L和弹力F的大小关系图线,试由图线确定: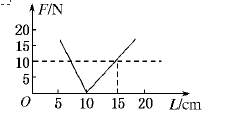
(1)弹簧的原长;
(2)弹簧的劲度系数;
(3)弹簧伸长0.15 m时,弹力的大小.
如图所示,半径为R､内壁光滑的空心圆筒放在地上,将两个重力都是G､半径都是r的球(R<2r<2R)放在圆筒中,求:
(1)筒底对球A的弹力?
(2)筒壁对球A的弹力是否大于筒壁对球B的弹力?
(3)球A对球B的弹力一定大于重力G吗?
(4)球B对筒壁的压力一定小于重力G吗?
(8分)如图，光滑水平面AB与竖直面的半圆形导轨在B点相连接，导轨半径为R，一质量为m的静止木块在A处压缩弹簧，释放后，木块获得一向右的初速度，当它经过B点进入导轨瞬间对导轨的压力是其重力的7倍，之后向上运动恰能通过轨道顶点C，不计空气阻力，试求：
(1)弹簧对木块所做的功；
(2)木块从B到C过程中克服摩擦力做的功；
(12分)人拉原来静止的重300N的车在水平路面上前进,拉力大小为20N,方向斜向上且与水平方向成300角,车前进500米,车与路面的动摩擦因数为0.03,求:
(1)拉力对车所做的功;
(2)摩擦力对车所做的功;
(3)车获得的动能.