如图所示，在坐标原点O处，能向四周均匀发射速度大小相等、方向都平行于纸面的带正电粒子。在O点右侧有一半径为R的圆形薄板，薄板中心O′位于x轴上，且与x轴垂直放置，薄板的两端M、N与原点O正好构成等腰直角三角形。已知带电粒子的质量为m，带电量为q，速率为v，重力不计。
（1）要使y轴右侧所有运动的粒子都能打到薄板MN上，可在y轴右侧加一平行于x轴的匀强电场，则场强的最小值E0为多大？在电场强度为E0时，打到板上的粒子动能为多大?
（2）要使薄板右侧的MN连线上都有粒子打到，可在整个空间加一方向垂直纸面向里的匀强磁场，则磁场的磁感应强度不能超过多少（用m、v、q、R表示）?若满足此条件，从O点发射出的所有带电粒子中有几分之几能打在板的左边?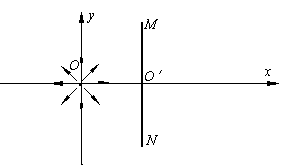
冬季有一种雪上“府式冰撬”滑溜运动，运动员从起跑线推着冰撬加速一段相同距离，再跳上冰撬自由滑行，滑行距离最远者获胜，运动过程可简化为如图所示的模型，某一质量m="20" kg的冰撬静止在水平雪面上的A处，现质量M=60kg的运动员，用与水平方向成α=37°角的恒力F="200" N斜向下推动冰撬，使其沿AP方向一起做直线运动，当冰撬到达P点时运动员迅速跳上冰撬与冰撬一起运动（运动员跳上冰撬瞬间，运动员和冰撬的速度不变）。已知冰撬从A运动到P的运动时间为2s，冰撬与雪面间的动摩擦因数为0.2，不计冰撬长度和空气阻力。（g取10 m/s2，cos 37°=0.8）求：
（1）AP的距离；
（2）冰撬从P点开始还能继续滑行多远?
质量为2kg的平板车B上表面水平，原来静止在光滑水平面上，平板车一端静止着一块质量为2kg的物体A，A和B 之间的动摩擦因数
。一颗质量为0．01kg的子弹以600m/s的速度水平瞬间射穿A后，速度变为200m/s。若A不会滑离B，求平板车B的长度至少为多少？；
图所示是一列沿
轴正方向传播的简谐横波在
时刻的波形图，已知波的传播速度
，试回答下列问题：
（1）求出
处的质点在
内通过的路程及 
时该质点的位移；
（2）写出
处的质点的振动函数表达式。
如图所示，一圆柱形绝热容器竖直放置，通过绝热活塞封闭着摄氏温度为t1的理想气体，活塞的质量为m，横截面积为S，与容器底部相距h1。现通过电热丝给气体加热一段时间，使其温度上升到（摄氏）t2，若这段时间内气体吸收的热量为Q，已知大气压强为p0，重力加速度为g，求：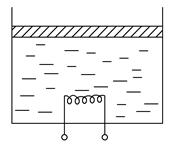
(1)气体的压强．
(2)这段时间内活塞上升的距离是多少？
(3)这段时间内气体的内能如何变化，变化了多少？
图所示，在坐标系
右侧存在一宽度为
、垂直纸面向外的有界匀强磁场，磁感应强度的大小为B；在左侧存在与y轴正方向成
角的匀强电场。一个粒子源能释放质量为m、电荷量为+q的粒子，粒子的初速度可以忽略。粒子源在点P(
，)时发出的粒子恰好垂直磁场边界EF射出；将粒子源沿直线PO移动到Q点时，所发出的粒子恰好不能从EF射出。不计粒子的重力及粒子间相互作用力。求：
（1）匀强电场的电场强度；
（2）粒子源在Q点时，粒子从发射到第二次进入磁场的时间。