如图所示,有一水平桌面长L,套上两端开有小孔的外罩(外罩内情况无法看见),桌面上沿中轴线有一段长度未知的粗糙面,其它部分光滑,一小物块(可视为质点)以速度 从桌面的左端沿桌面中轴线方向滑入,小物块与粗糙面的动摩擦系数μ=1/2,小物体滑出后做平抛运动,桌面离地高度h以及水平飞行距离s均为
从桌面的左端沿桌面中轴线方向滑入,小物块与粗糙面的动摩擦系数μ=1/2,小物体滑出后做平抛运动,桌面离地高度h以及水平飞行距离s均为 (重力加速度为g)求:
(重力加速度为g)求: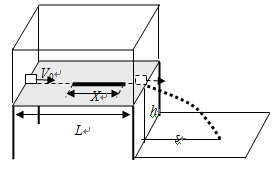
(1)未知粗糙面的长度X为多少?
(2)若测得小物块从进入桌面到落地经历总时间为 ,则粗糙面前端离桌面最左端的距离?
,则粗糙面前端离桌面最左端的距离?
(3)粗糙面放在何处,滑块滑过桌面用时最短,该时间为多大?
如图所示电路中,R1=0.8Ω,R3=6Ω,滑动变阻器的全值电阻R2="12" Ω,电源电动势E="6" V,内阻r="0.2" Ω,当滑动变阻器的滑片在变阻器中央位置时,闭合开关S,电路中的电流表和电压表的读数各是多少?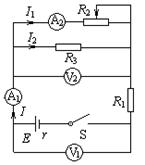
如右图所示,在某空间实验室中,有两个靠在一起的等大的圆柱形区域,分别存在着等大反向的匀强磁场,磁感应强度B=0.10 T,磁场区域半径r=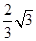 m,左侧区圆心为O1,磁场向里,右侧区圆心为O2,磁场向外.两区域切点为C.今有质量m=3.2×10-26 kg.带电荷量q=1.6×10-19 C的某种离子,从左侧区边缘的A点以速度v=106 m/s正对O1的方向垂直磁场射入,它将穿越C点后再从右侧区穿出.求:
m,左侧区圆心为O1,磁场向里,右侧区圆心为O2,磁场向外.两区域切点为C.今有质量m=3.2×10-26 kg.带电荷量q=1.6×10-19 C的某种离子,从左侧区边缘的A点以速度v=106 m/s正对O1的方向垂直磁场射入,它将穿越C点后再从右侧区穿出.求:
(1)该离子通过两磁场区域所用的时间.
(2)离子离开右侧区域的出射点偏离最初入射方向的侧移距离为多大?(侧移距离指垂直初速度方向上移动的距离)
如图所示,真空中有以O′为圆心,r为半径的圆柱形匀强磁场区域,圆的最下端与x轴相切于坐标原点O,圆的右端与平行于y轴的虚线MN相切,磁感应强度为B,方向垂直纸面向外,在虚线MN右侧x轴上方足够大的范围内有方向竖直向下、场强大小为E的匀强电场.现从坐标原点O向纸面内不同方向发射速率相同的质子,质子在磁场中做匀速圆周运动的半径也为r,已知质子的电荷量为e,质量为m,不计质子的重力、质子对电磁场的影响及质子间的相互作用力.求:
(1)质子进入磁场时的速度大小;
(2)沿y轴正方向射入磁场的质子到达x轴所需的时间.
11.(18分)如图所示,直角坐标系xOy位于竖直平面内,在水平的x轴下方存在匀强磁场和匀强电场,磁场的磁感应为B,方向垂直xOy平面向里,电场线平行于y轴。一质量为m、电荷量为q的带正电的小球,从y轴上的A点水平向右抛出,经x轴上的M点进入电场和磁场,恰能做匀速圆周运动,从x轴上的N点第一次离开电场和磁场,MN之间的距离为L,小球过M点时的速度方向与x轴的方向夹角为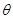 .不计空气阻力,重力加速度为g,求
.不计空气阻力,重力加速度为g,求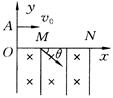
(1)电场强度E的大小和方向;
(2)小球从A点抛出时初速度v0的大小;
(3)A点到x轴的高度h.
25.(18分)如图所示,在0≤x≤a、o≤y≤ 范围内有垂直于xy平面向外的匀强磁场,磁感应强度大小为B。坐标原点O处有一个粒子源,在某时刻发射大量质量为m、电荷量为q的带正电粒子,它们的速度大小相同,速度方向均在xy平面内,与y轴正方向的夹角分布在0~90°范围内.己知粒子在磁场中做圆周运动的半径介于
范围内有垂直于xy平面向外的匀强磁场,磁感应强度大小为B。坐标原点O处有一个粒子源,在某时刻发射大量质量为m、电荷量为q的带正电粒子,它们的速度大小相同,速度方向均在xy平面内,与y轴正方向的夹角分布在0~90°范围内.己知粒子在磁场中做圆周运动的半径介于 到a之间,从发射粒子到粒子全部离开磁场经历的时间恰好为粒子在磁场中做圆周运动周期的四分之一,求最后离开磁场的粒子从粒子源射出时的:
到a之间,从发射粒子到粒子全部离开磁场经历的时间恰好为粒子在磁场中做圆周运动周期的四分之一,求最后离开磁场的粒子从粒子源射出时的:
(1)速度大小;
(2)速度方向与y轴正方向夹角正弦。